FROM THE GIVEN TRANSFORMATION FIND THE QUADRATIC FUNCTION

Problem 1 :

Write a quadratic equation with a minimum that has been shifted 5 units to the right and 7 units down from the parent function.

Solution:

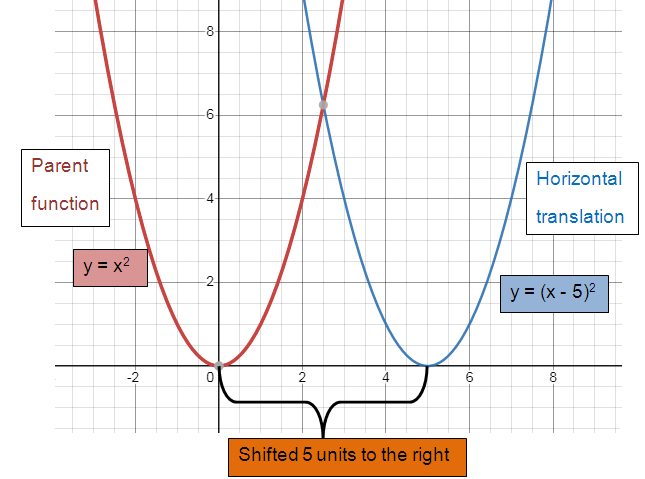
Parent function y = x²

Horizontal translation:

Shifted 5 units to the right.

y = (x - 5)² 

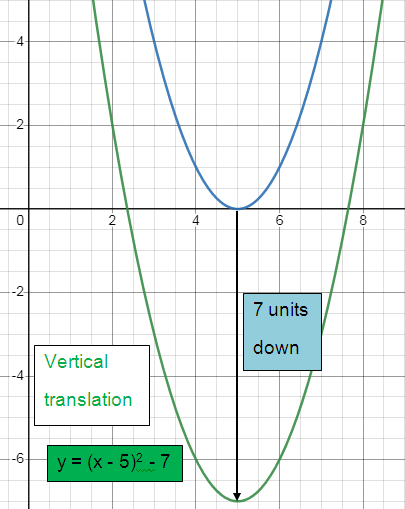
Vertical translation:

Shifted 7 units to the down.

y = (x - 5)² - 7

Problem 2 :

Write a quadratic equation with a maximum that has been shifted 4 units to the left and 3 units up from the parent function.

Solution:

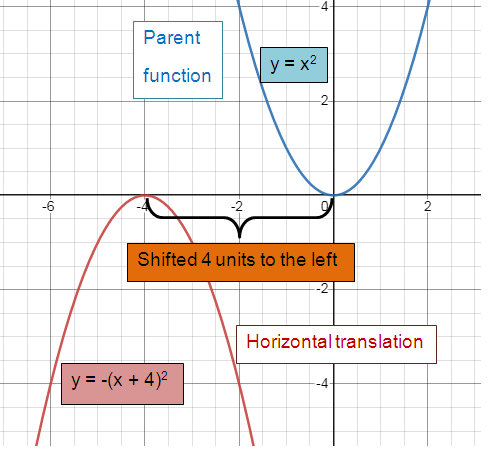
Parent function y = x²

Horizontal translation:

Shifted 4 units to the left.

y = -(x + 4)²

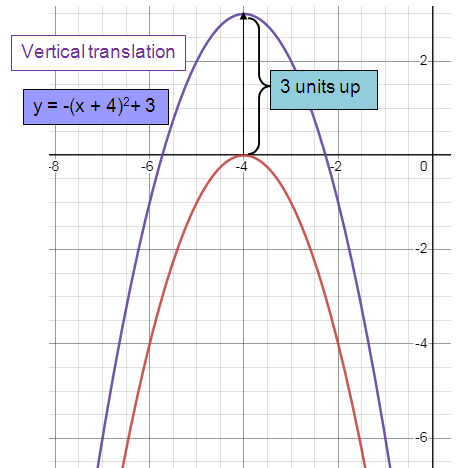
Vertical translation:

Shifted 3 units to the up.

y = -(x + 4)² + 3

Problem 3 :

Write a quadratic equation with a maximum that has been shifted 2 units to the right and 1 units down from the parent function.

Solution:

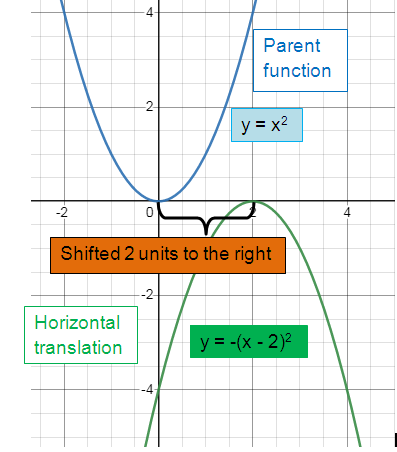
Parent function y = x²

Horizontal translation:

Shifted 2 units to the right.

y = -(x - 2)² 

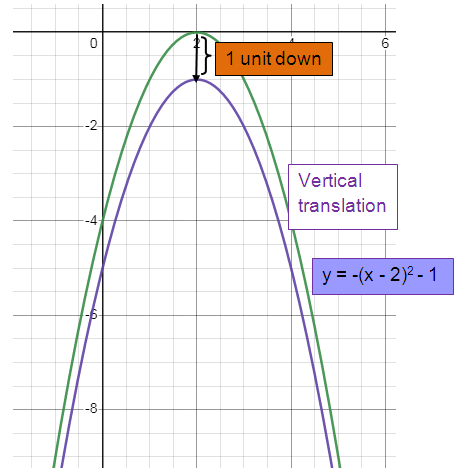
Vertical translation:

Shifted 1 unit to the down.

y = -(x - 2)² - 1

Problem 4 :

Write a quadratic equation with a minimum that has been shifted 5 units to the left and 6 units down from the parent function.

Solution:

Parent function y = x²

Shifted 5 units to the left and 6 units down.

y = (x + 5)² - 6

Problem 5 :

What is the equation of this graph?

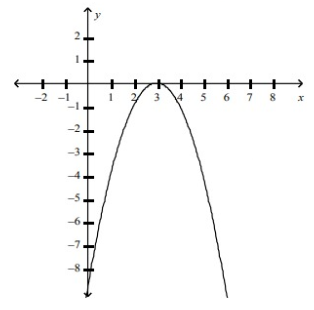
a. y = -x² + 3       b. y = -3x²        c. y = -(x + 3)²

d. y = -(x - 3)²

Solution:

In the above graph, shifted 3 units to the right and no vertical movement from the parent function. So,

y = -(x - 3)²

So, option (d) is correct.

Problem 6 :

Which function includes a translation of 3 units to the left?

a. f(x) = (x + 3)² + 1         b. f(x) = 3x² + 1

c. f(x) = (x - 3)² + 1          d. f(x) = (x + 1)² - 3

Solution:

Parent function y = x²

Translation of 3 units to the left

f(x) = (x + 3)² 

So, option (a) is correct.

Problem 7 :

Which equation shows a translation of 3 left and vertical compression by a factor of 2 to the graph of y = x² ?

Solution:

a. y = 2(x - 3)²        b. y = 2(x + 3)²

Solution:

Parent function y = x²

After translation

y = 2(x + 3)²

So, option (b) is correct.

Problem 8 :

Which equation describes a parabola that opens downward, is congruent to y = x², and has its vertex at (0, 3)?

a. y = (x + 3)² - 1         b. y = -x² + 3

c. y = -(x - 3)²                 d. y = x² + 3

Solution:

vertex (0, 3)

a.

y = (x + 3)² - 1

when x = 0, y = 8

b. 

y = -x² + 3

when x = 0, y = 3

c. 

y = -(x - 3)²

when x = 0, y = -9

d.

y = x² + 3

when x = 0, y = 3

It is congruent to y = x².

So, option (d) is correct.

Problem 9 :

List the sequence of steps required to graph the function

f(x) = -(x + 4)² - 6

a. Horizontal translation 4 units to the right, vertical compression by a factor of 1, vertical translation 6 units down.

b. Horizontal translation 4 units to the right, reflection in x-axis, vertical translation 6 units down.

c. horizontal translation 4 units to the left, vertical translation 6 units up, reflection in x-axis.

d. horizontal translation 4 units to the left, reflection in x-axis, vertical translation 6 units down.

Solution:

f(x) = -(x + 4)² - 6

Parent function y = x²

Shift 4 units to the left, reflect across the x-axis, shift 6 units downwards.

So, option (d) is correct.

Problem 10 :

Which function matches the graph?

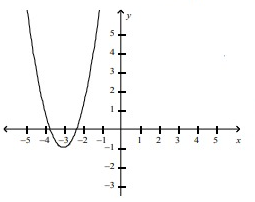
a. f(x) = -2(x - 3)² + 1       b. f(x) = 2(x + 3)² - 1

c. f(x) = (x + 3)² + 2

Solution:

In above graph, horizontal translation 3 units to the left, vertical compression by a factor of 2, vertical translation 1 unit down.

f(x) = 2(x + 3)² - 1

So, option (b) is correct.

Problem 11 :

Consider a parabola P that is congruent to y = x², opens upward, and has vertex (-1, 3). Now find the equation of a new parabola that results if P is reflected in the x-axis and translated 3 units down.

a. y = -(x + 4)² + 3       b. y = (x - 1)² + 6

c. y = -(x + 1)²             d. y = -(x - 2)² + 3

Solution:

Parent function is y = x²

Opens upward and it has vertex (-1, 3).

y = (x - (-1))² + 3

y = (x + 1)² + 3

Reflection across the x-axis. Then put y = -y

y = -(x + 1)² + 3

Translating 3 units down :

y = -(x + 1)² + 3 - 3

y = -(x + 1)² 

So, option c is correct.