FROM THE GIVEN RELATION PAIR FIND FOG AND GOF

Problem 1 :

Functions f and g are defined as follows :

f = {(0, 2), (1, 3), (2, 0), (3, 1)}

g = {(0, 3), (1, 2), (2, 1), (3, 0)}

Find a) f ∘ g

b) g ∘ f

c) f ∘ f

Solution :

a) f ∘ g

f = {(0, 2), (1, 3), (2, 0), (3, 1)}

From the given relation of f, drawing the arrow diagram.

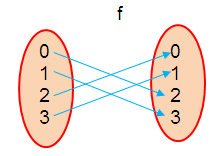
g = {(0, 3), (1, 2), (2, 1), (3, 0)}

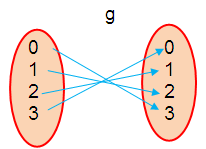
a) Finding fog :

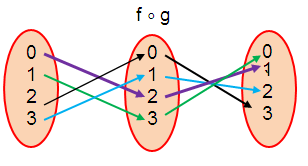
(f ∘ g) (0) = 1

(f ∘ g) (1) = 0

(f ∘ g) (2) = 3

(f ∘ g) (3) = 2

f ∘ g = {(0, 1), (1, 0), (2, 3), (3, 2)}

b) Finding gof :

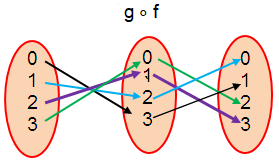
(g ∘ f) (0) = 1

(g ∘ f) (1) = 0

(g ∘ f) (2) = 3

(g ∘ f) (3) = 2

g ∘ f = {(0, 1) (1, 0) (2, 3) (3, 2)}

c) Finding fof :

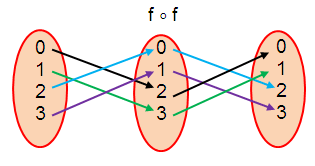
(f ∘ f) (0) = 0

(f ∘ f) (1) = 1

(f ∘ f) (2) = 2

(f ∘ f) (3) = 3

f ∘ f = {(0, 0), (1, 1), (2, 2), (3, 3)}

Problem 2 :

f and g are defined as :

f = {(0, 3), (1, 0), (2, 1), (3, 2)}

g = {(0, 1), (1, 2), (2, 3), (3, 0)}

Find f ∘ g

Solution :

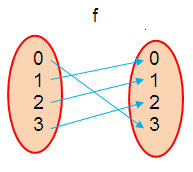
f = {(0, 3), (1, 0), (2, 1), (3, 2)}

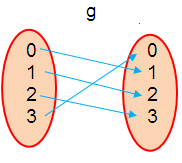
g = {(0, 1), (1, 2), (2, 3), (3, 0)}

Finding fog :

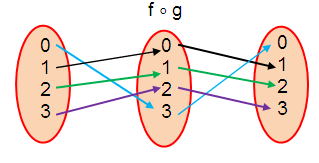
(f ∘ g) (0) = 0

(f ∘ g) (1) = 1

(f ∘ g) (2) = 2

(f ∘ g) (3) = 3

f ∘ g = {(0, 0), (1, 1), (2, 2), (3, 3)}

Problem 3 :

f and g are defined as :

f = {(0, 2), (1, 5), (2, 7), (3, 9)}

g = {(2, 2), (5, 0), (7, 1), (9, 3)}

Find a) f ∘ g    b) g ∘ f

Solution :

f = {(0, 2), (1, 5), (2, 7), (3, 9)}

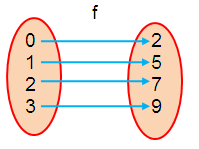
g = {(2, 2), (5, 0), (7, 1), (9, 3)}

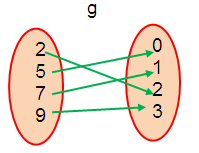
a) Finding  f ∘ g :

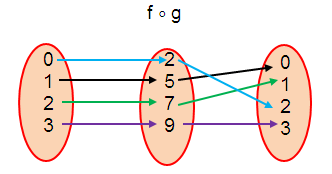
(f ∘ g) (0) = 2

(f ∘ g) (1) = 0

(f ∘ g) (2) = 1

(f ∘ g) (3) = 3

f ∘ g = {(0, 2), (1, 0), (2, 1), (3, 3)}

b) Finding  g ∘ f :

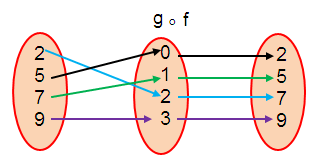
(g ∘ f) (2) = 7

(g ∘ f) (5) = 2

(g ∘ f) (7) = 5

(g ∘ f) (9) = 9

g ∘ f = {(2, 7), (5, 2), (7, 5), (9, 9)}

Problem 4 :

a) If ax + b = cx + d for all values of x, show that a = c and b = d.

Hint : if it is true for all x, it is true for x = 0 and x = 1.

b) Given, f(x) = 2x + 3 and g(x) = ax + b and that (f ∘ g) (x) = x for all values of x, deduce that a = 1/2 and b = -3/2.

c) Is the result in b true if (g ∘ f) (x) = x for all x ?

Solution :

a)

ax + b = cx + d

Let, x = 0

b = d

ax + d = cx + d

Subtracting d on both sides.

ax = cx for all x.

Let, x = 1

a = c

b. Given, f(x) = 2x + 3 and g(x) = ax + b

(f ∘ g) (x) = x for all values of x,

f(g(x))  = x

2(ax + b) + 3 = x

2ax + 2b + 3 = x

2ax – x = -2b – 3

x(2a -1) = -2b – 3, for all x.

c) Given, f(x) = 2x + 3 and g(x) = ax + b and that (g ∘ f) (x) = x

g(f(x)) = x

g(2x + 3) = x

a(2x + 3) + b = x

2ax + 3a + b = x

2ax – x = -3a – b

x(2a – 1) = -3a – b

So, the result in b is true.