FROM THE GIVEN ORDERED PAIR HOW TO CHECK IT IS FUNCTION OR NOT

Linear function :

In linear relationship, the change will be equal and constant. To get every y-value, we have to add or subtract some constant.

Exponential function :

In exponential relationship, the change will be equal and constant. To get every y-value, we have to multiply or divide some constant.

Tell whether the points appear to represent a linear function, or exponential function or neither.

Problem 1 :

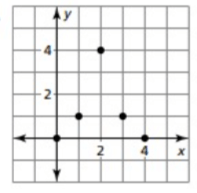
Solution :

Ordered pairs :

(0, 0) (1, 1) (2, 4) (3, 1) (4, 0)

By observing the values of y, we don't see that a non zero number is multiplied or divided by anything. So, it is not a exponential function.

Problem 2 :

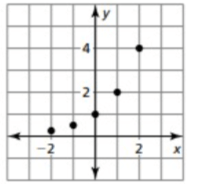
Solution :

By connecting the set of points in the graph, we get the exponential growth curve.

Problem 3 :

(2, 1/16) (1, 1/4) (0, 1) (-1, 4) (-2, 16)

Solution :

By observing the values of x, it increases gradually.

From the given ordered pairs, by observing the values of y.

The multiplication factor is the same. So, it is exponential function with the scale factor of 1/4.

Problem 4 :

(-1, 5) (0, 0) (1, -1) (2, 0) and (3, 5)

Solution :

By observing the values of x, it increases gradually.

From the given ordered pairs, by observing the values of y.

Comparing (-1, 5) and (0, 0)

5 - 5 ==> 0

Comparing (0, 0) and (1, -1)

0 - 5 ==> -5 but it is -1

So, the factor is not the same. It is not linear or exponential function. So, it is neither.

Problem 5 :

(-4, -3) (-2, -2) (0, -1) (2, 0) and (4, 1)

Solution :

By observing the values of x, it increases gradually.

From the given ordered pairs, by observing the values of y.

Comparing (-4, -3) (-2, -2) :

-3 + 1 ==> -2

Comparing (-2, -2) and (0, -1) :

-2 + 1 ==> -1

Since we add the same value to get the value of y in the consequent ordered pair, it is linear function.

Problem 6 :

(-3, -6) (-2, -4) (-1, -2) (0, 0) and (1, 2)

Solution :

By observing the values of x, it increases gradually.

From the given ordered pairs, by observing the values of y.

Comparing (-3, -6) (-2, -4) :

-6 + 2 ==> -4

Comparing (-2, -4) and (-1, -2) :

-4 + 2 ==> -2

Since we add the same value to get the value of y in the consequent ordered pair, it is linear function.

Tell whether the table of values represents a linear or an exponential function. Then write the function.

Problem 7 :

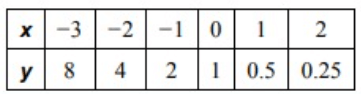
Solution :

By observing the values of x, it increases gradually.

From the given ordered pairs, by observing the values of y.

Here the scale factor is 2. So, it is exponential function. 

Problem 8 :

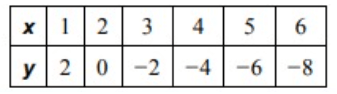
Solution :

By observing the values of x, it increases gradually.

From the given ordered pairs, by observing the values of y.

2 - 2 ==> 0

0 - 2 ==> -2

-2 - 2 ==> -4

Every time, we subtract 2. So, it is linear function.