FROM THE GIVEN INFORMATION FIND EQUATION OF HYPERBOLA

Find the standard form of the equation of each hyperbola.

Problem 1 :

Foci (0, ±4), vertices (0, ±2)

Solution:

 Foci = (0, ±4)

= (0, ±c)

c = 4

vertices = (0, ±a)

= (0, ±2)

a = 2

b² = c² - a²

= 4² - 2²

= 16 - 4

b² = 12

So, the equation of hyperbola is

Problem 2 :

Vertices (±4, 0), Asymptotes: y = ±3x

Solution:

Vertices (4, 0) (-4, 0)

The hyperbola is the horizontal transverse axis type.

Vertices = (±a, 0)

a = 4

So, the equation of hyperbola is

Problem 3 :

Endpoints of transverse axis: (±6, 0), Asymptotes: y = ±2x

Solution:

The hyperbola is the horizontal transverse axis type.

Here a = 6

So, the equation of hyperbola is

Problem 4 :

Foci (0, ±3), length of transverse axis 2

Solution:

Foci = (0, ±c)

c = 3

length of transverse axis 2a = 2

a = 1

b² = c² - a²

= 3² - 1²

= 9 - 1

b² = 8

So, the equation of hyperbola is

Problem 5 :

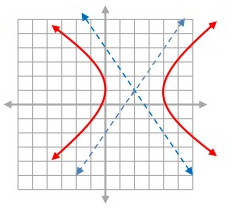
Solution:

From given graph, 

Center (h, k) = (2, 1)

Vertices = (4, 1) (0, 1)

a = 2

b = 3

So, the equation of hyperbola is

Problem 6 :

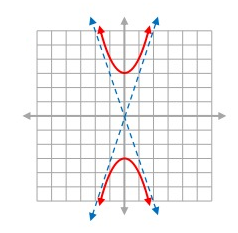
Solution:

From given graph, 

Center (h, k) = (0, 0)

Vertices = (3, 0) (-3, 0)

a = 3

b = 1

So, the equation of hyperbola is