FROM THE GIVEN GRAPH HOW TO CHECK IF THE FUNCTION IS ODD OR EVEN

Symmetric about y-axis

A graph has symmetry with respect to the y-axis if the following condition is true.

Before (x, y)

After (-x, y)

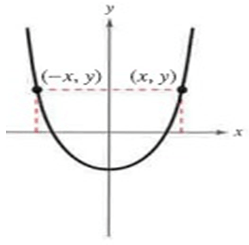
A function whose graph is symmetric with respect to the y-axis is an even function.

Symmetric about Origin

A graph has symmetry with respect to the origin if  the following condition is true.

Before (x, y)

After (-x, -y)

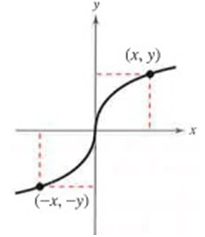
A function whose graph is symmetric with respect to the origin is an odd function.

Symmetric about x-axis

A graph has symmetry with respect to the x-axis if

Before (x, y)

After (x, -y)

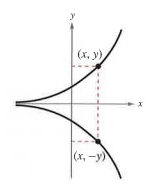
A graph that is symmetric with respect to the x-axis is not the graph of a function (except for the graph of y = 0).

For each graph, determine whether the function is even, odd, or neither.

Problem 1 :

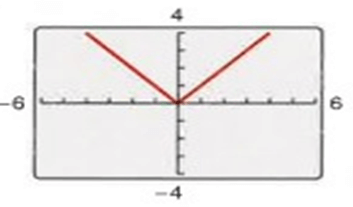
Solution :

The given curve is graph of absolute value function, tracing some of the points on the curve,

Corresponding point of (1, 1) ==>  (-1, 1)

Corresponding point of (2, 2) ==>  (-2, 2),..... etc

The graph is symmetric with respect to the y-axis. So, the function is even.

Problem 2 :

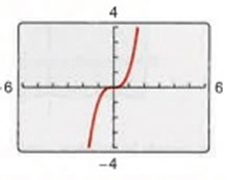
Solution :

The curve is passing through origin. Tracing some of the point on the curve,

corresponding point of (1, 1) ==> (-1, -1)

corresponding point of (2, 2) ==> (-2, -2),..... etc

The graph is symmetric with respect to the origin. So, the function is odd.

Problem 3 :

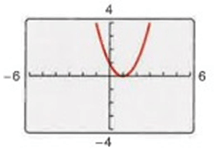
Solution :

The graph is not symmetric about origin, because tracing some of the points on the curve, they are not in the form of 

(x, y) ==> (-x, -y)

The graph is neither symmetric with respect to the origin.

It is not symmetric about y-axis, because tracing some of the points,

Corresponding point of (2, 1) is not (-2,1). At (-2, 1), we dont have curve. 

So, the function is neither even nor odd.

Problem 4 :

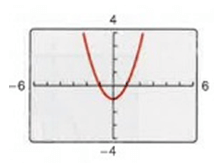
Solution :

Tracing some of the points on the curve,

corresponding point of (1, 0) ==> (-1, 0)

corresponding point of (2, 2) ==> (-2, 2)

The graph is symmetric with respect to the y-axis. So, the function is even.