FROM THE GIVEN GRAPH FIND THE INVERSE GRAPH
To draw the graph of inverse from the graph of original function, we have to follow the procedure given below.
Step 1 :
Mark the points from the given graph. The set of ordered pairs from the graph will be in the form of (x, y).
Step 2 :
To find the coordinates of inverse function, we have to exchange the values of x and y. So, we will get the set of ordered pairs in the form of (x, y). But these are the points for the inverse function.
That is,
Domain of f(x) = Range of f-1(x)
Range of f(x) = Domain of f-1(x)
Use the graph of the function f to create a table of values for the given points. Then create a second table that can be used to find f-1, and sketch the graph of f-1 if possible.
Problem 1 :
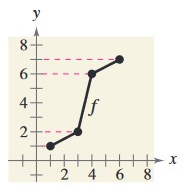
Solution:
Points from the given graph f(x).
|
x 1 3 4 6 |
y 1 2 6 7 |
Writing the values of f(x) as set of ordered pairs :
(1, 1) (3, 2) (4, 6) and (6, 7)
Inverse function:
Let f-1(x) be the inverse of the given function f(x). To get the coordinates of inverse function, we have to exchange the values of x and y.
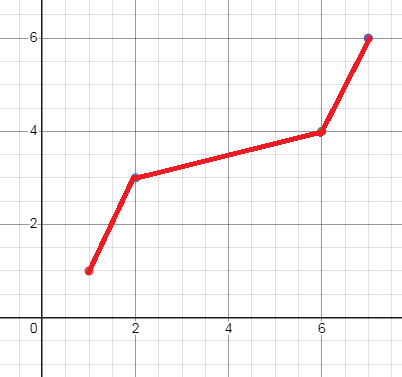
Points to the plotted to make inverse function.
|
x 1 2 6 7 |
y 1 3 4 6 |
Writing the values of f-1(x) as set of ordered pairs :
(1, 1) (2, 3) (6, 4) and (7, 6)
Problem 2 :
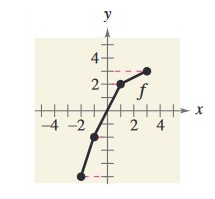
Solution:
Points from the given graph f(x).
|
x -2 -1 1 3 |
y -5 -2 2 3 |
Writing the values of f(x) as set of ordered pairs :
(-2, -5) (-1, -2) (1, 2) (3, 3)
Inverse function:
Let f-1(x) be the inverse of the given function f(x). To get the coordinates of inverse function, we have to exchange the values of x and y.
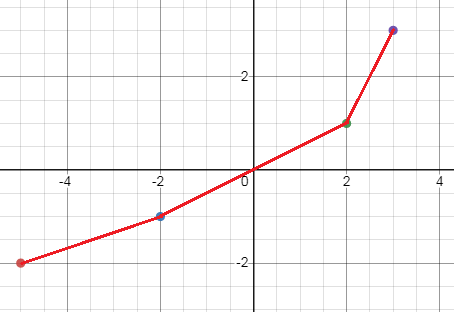
Points to the plotted to make inverse function.
|
x -5 -2 2 3 |
y -2 -1 1 3 |
Writing the values of f-1(x) as set of ordered pairs :
(-5, -2) (-2, -1) (2, 1) (3, 3)
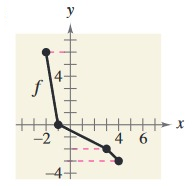
Problem 3 :
Solution:
Points from the given graph f(x).
|
x 3 4 -1 -2 |
y -2 -3 0 5 |
Writing the values of f(x) as set of ordered pairs :
(3, -2) (4, -3) (-1, 0) (-2, 5)
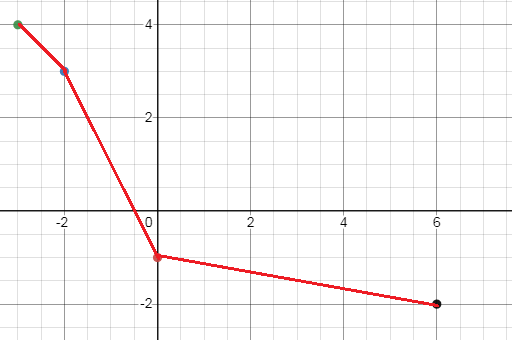
Inverse function:
Let f-1(x) be the inverse of the given function f(x). To get the coordinates of inverse function, we have to exchange the values of x and y.
Points to the plotted to make inverse function.
|
x -2 -3 0 5 |
y 3 4 -1 -2 |
Writing the values of f-1(x) as set of ordered pairs :
(-2, 3) (-3, 4) (0, -1) (5, -2)
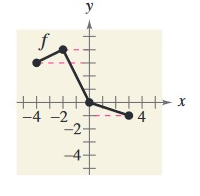
Problem 4 :
Solution:
Points from the given graph f(x).
|
x -4 -2 0 3 |
y 3 4 0 -1 |
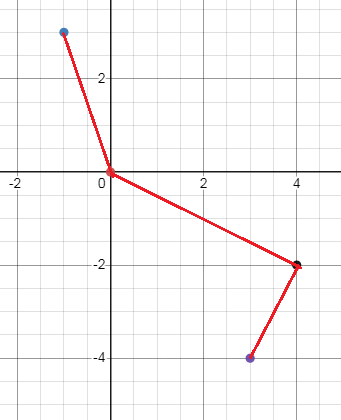
Inverse function:
Let f-1(x) be the inverse of the given function f(x). To get the coordinates of inverse function, we have to exchange the values of x and y.
Points to the plotted to make inverse function.
|
x 3 4 0 -1 |
y -4 -2 0 3 |
Writing the values of f-1(x) as set of ordered pairs :
(3, -4) (4, -2) (0, 0) (-1, 3)
Sketch the inverse of the function graphed and the line of reflection What is the domain and range of the original function and it’s inverse
Problem 5 :
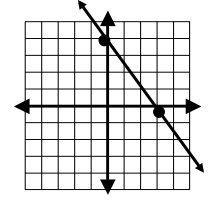
Solution :
Marking the points from the given line, we get
(0, 4) and (3, 0)
Points for the inverse function :
(4, 0) and (0, 3)
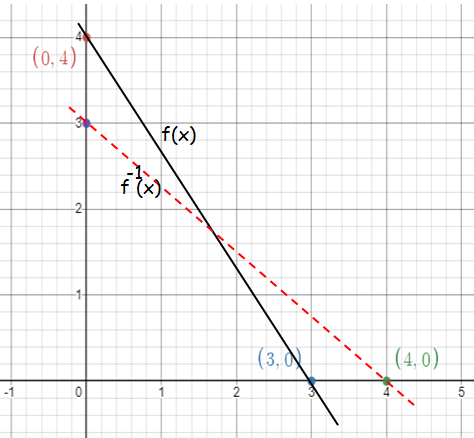
Problem 6 :
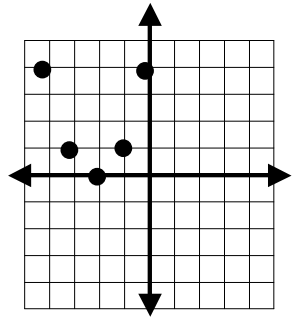
Solution :
Marking the points from the given line, we get
(-3, 1)(-1, 1) (-2, 0) (-4, 4) (0, 4)
Points for the inverse function :
(1, -3)(1, -1) (0, -2) (4, -4) (4, 0)
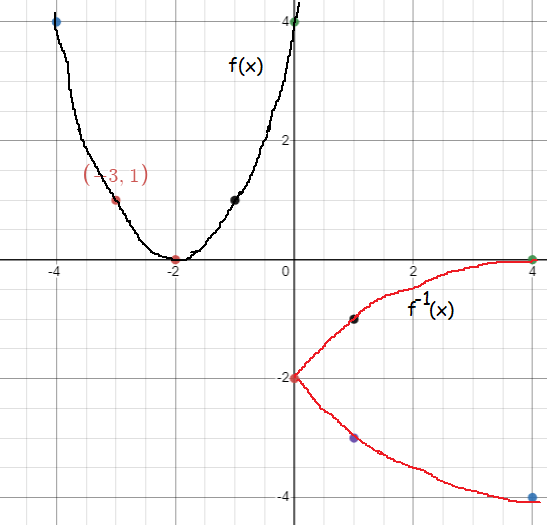
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling