FOUNDATION OF FUNCTIONS

Problem 1 :

Domain: {x| x ≥ 0, x ≠ 2} Range: {y|-3 < y ≤ 3} Which graph corresponds to the given constraints?

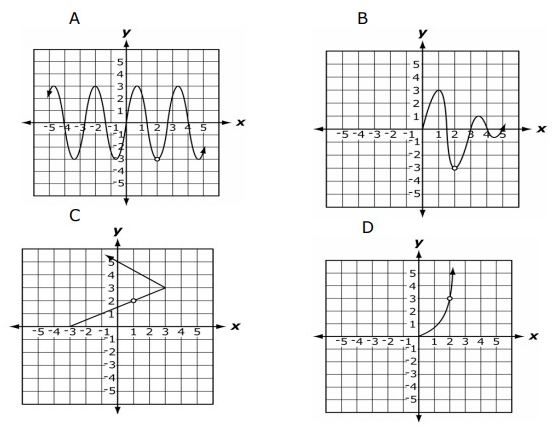
Solution:

Domain : {x| x ≥ 0, x ≠ 2} Range: {y|-3 < y ≤ 3}

Understanding the domain :

Values of x should be greater than or equal to 0 except 2. Which means, we can take positive values only, we should not include 2.

Understanding range :

The minimum value of y should be greater than -3 and its maximum value should be 3.

Option (B) is correct.

Problem 2 :

Tyrone wants to spend at most $10,000 on two televisions, R and S. Each television must cost at least $3,000, and television R must cost at least twice as much as television S. Which system of inequalities models the amount of money spent on each television?

Solution:

Tyrone want at most 10,000, two TV. R and S

R + S ≤ 10,000

Each television atleast $3,000.

R ≥ 3,000

S  ≥ 3,000

Television R at least twice as much as television S.

R  ≥ 2S

So, option (C) is correct.

Problem 3 :

Meredith invests $50,000 in her new business. It costs the company $10 to produce each unit, which is sold for $15. Let C represent the cost and R represent the revenue for x units. Which statement is true about the graphs of the equations

C = 50,000 + 10x and R = 15x ?

A) Both slopes are positive.

B) Both slopes are negative.

C) One slope is positive, and the other is zero.

D) One slope is negative, and the other is positive.

Solution:

C = 50,000 + 10x

R = 15x

Both C and R represent a linear graph.

y = mx + c

m = slope

c = 10x + 50,000

By comparison, 

m = 10 = slope and R = 15x

By comparison, 

m = 15 = slope 

The statement that is true is that both slopes are positive.

So, statement (A) is correct.

Problem 4 :

Which graph represents the inverse of f(x) = 2x?

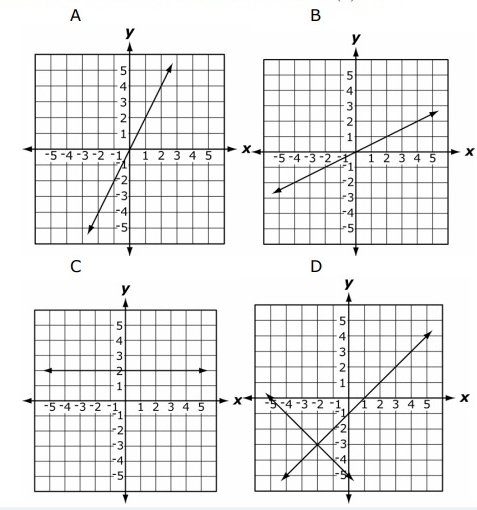
Solution:

f(x) = 2x

Let f(x) = y

x = f^-1(y)

y = 2x

x = y/2

f^-1(y) = y/2

f^-1(x) = x/2

Since it is a line passes through origin with slope 1/2. Option (B) is the graph for inverse of f(x) = 2x.

Problem 5 :

How many real roots does the function given by the graph have?

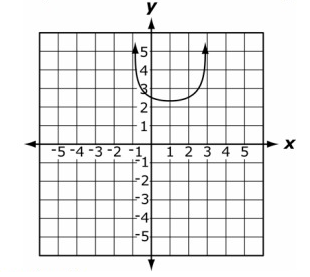
A. 0 real roots    B. 1 real root    C. 2 real roots

D. 4 real roots

Solution:

The above graph of the function cross points of y-axis only at a certain point.

Therefore, the function only has 1 real root.

So. option (B) is correct.

Problem 6 :

What number is added to both sides of the equation

x² - 8x + 3 = 0

to solve it by completing the square?

A. -16      B. 16     C. -64      D. 64

Solution:

So, option (B) is correct.

Problem 7 :

What is the inverse of f(x) = x + 1?

A. f^-1(x) = -x - 1

B. f^-1(x) = x - 1

Solution:

f(x) = x + 1

Let f(x) = y

y = x + 1

Interchange the x and y.

x = y + 1

y = x - 1

Therefore, the inverse function of f(x) is f^-1(x) = x - 1.

So, option (B) is correct.

Problem 8 :

What is the inverse of the function f(x) = (x + 4)²?

Solution:

f(x) = (x + 4)²

Let f(x) = y

y = (x + 4)²

Interchange x and y.

x = (y + 4)²

y + 4 = ±√x

y = ±√x - 4

Therefore, the inverse function of f(x) is f^-1(x) = ±√x - 4.

So, option (C) is correct.