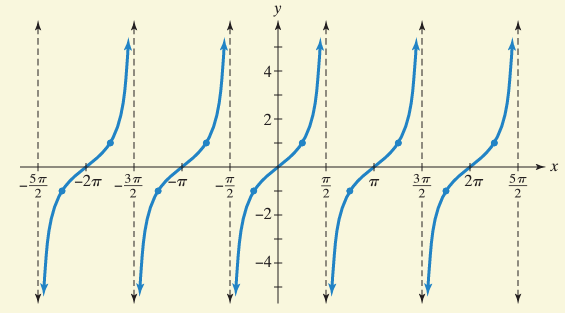
FINDING VERTICAL ASYMPTOTES OF TANGENT FUNCTIONS WITH TRANSFORMATIONS
For the function y = tan x, vertical asymptotes are odd multiples of π/2.
We use the characteristics of the tangent curve to graph tangent functions of the form y = A tan (Bx- C), where B > 0
To find the vertical asymptotes of tangent function, we follow the given steps.
Step 1 :
Find two consecutive asymptotes by finding an interval containing one period.
A pair of consecutive asymptotes occurs at
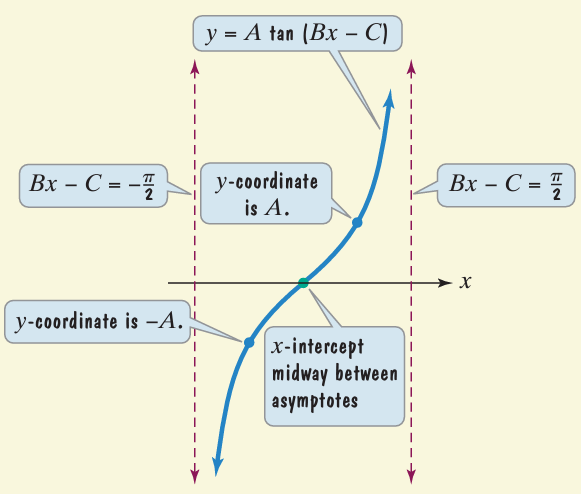
Vertical asymptote
for y = tan x is k𝜋 + 𝜋/2 , where k is integer
While equating Bx - C to k𝜋 + 𝜋/2, we will get more asymptotes.
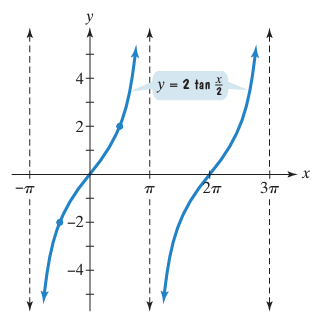
Graph the following tangent function. Find A, the period and the asymptotes.
Problem 1 :
y = 2 tan (x/2)
Solution :
A = 2
Consecutive asymptotes :
Find two consecutive asymptotes, we do this by finding an interval containing one period.
The period :
An interval containing one period is (-𝜋, 𝜋).
Thus two consecutive asymptotes occur at x = -𝜋 and x = 𝜋.
Finding consecutive asymptotes :
Vertical asymptote of y = tan x is k𝜋 + 𝜋/2, where k is integer. Here
Bx - C = x/2, then
x/2 = k𝜋 + 𝜋/2
x = 2(k𝜋 + 𝜋/2)
x = 2k𝜋 + 𝜋
x = 𝜋(2k + 1)
- When k = -1, x = -𝜋
- When k = 0, x = 𝜋
- When k = 1, x = 3𝜋
- When k = 2, x = 5𝜋
So, the required asymptotes for the given function are
-𝜋, 𝜋, 3𝜋, 5𝜋,.............
Problem 2 :
y = tan (x - (𝜋/4))
Solution :
A = 1
Consecutive asymptotes :
Find two consecutive asymptotes, we do this by finding an interval containing one period.
The period :
An interval containing one period is (-𝜋/4, 3𝜋/4).
Thus two consecutive asymptotes occur at x = -𝜋/4 and x = 3𝜋/4.
Finding consecutive asymptotes :
Vertical asymptote of y = tan x is k𝜋 + 𝜋/2, where k is integer. Here
Bx - C = x - (𝜋/4), then
x - (𝜋/4) = k𝜋 + 𝜋/2
x = k𝜋 + 𝜋/2 + (𝜋/4)
x = k𝜋 + 3𝜋/4
x = 𝜋(k + 3/4)
x = (𝜋/4)(4k + 3)
- When k = -1, x = -𝜋/4
- When k = 0, x = 3𝜋/4
- When k = 1, x = 7𝜋/4
- When k = 2, x = 11𝜋/4
So, the required asymptotes for the given function are
-𝜋/4, 3𝜋/4, 7𝜋/4, 11𝜋/4, .............

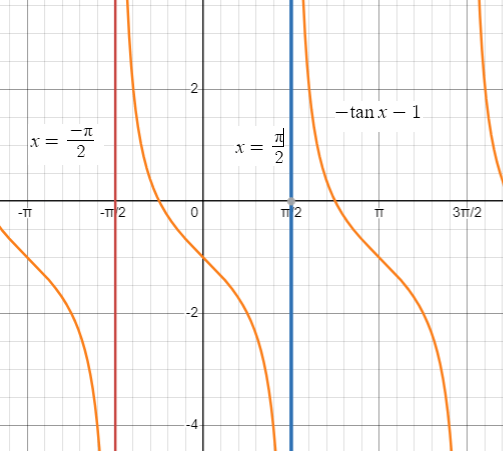
Problem 3 :
y = -tan x - 1
Solution :
y = -(tan x + 1)
A = 1
Since we have negative sign, there should be reflection across y-axis.
Consecutive asymptotes :
Find two consecutive asymptotes, we do this by finding an interval containing one period.
The period :
An interval containing one period is (-𝜋/2, 𝜋/2).
Thus two consecutive asymptotes occur at x = -𝜋/2 and x = 𝜋/2
Finding consecutive asymptotes :
Vertical asymptote of y = tan x is k𝜋 + 𝜋/2, where k is integer. Here
Bx - C = x , then
x = k𝜋 + 𝜋/2
- When k = -1, x = -𝜋/2
- When k = 0, x = 𝜋/2
- When k = 1, x = 3𝜋/2
- When k = -2, x = 5𝜋/2
Asymptotes are all odd multiples
Problem 4 :
y = tan (x - 𝜋)
Solution :
y = tan (x - 𝜋)
Standard form of tangent function with transformation is
y = A tan (Bx - C)
A = 1
Consecutive asymptotes :
Find two consecutive asymptotes, we do this by finding an interval containing one period.
The period :
An interval containing one period is (𝜋/2, 3𝜋/2).
Thus two consecutive asymptotes occur at x = 𝜋/2 and x = 3𝜋/2.
Finding consecutive asymptotes :
Vertical asymptote of y = tan x is k𝜋 + 𝜋/2, where k is integer. Here
Bx - C = x , then
x = k𝜋 + 𝜋/2
- When k = -1, x = -𝜋/2
- When k = 0, x = 𝜋/2
- When k = 1, x = 3𝜋/2
- When k = -2, x = 5𝜋/2
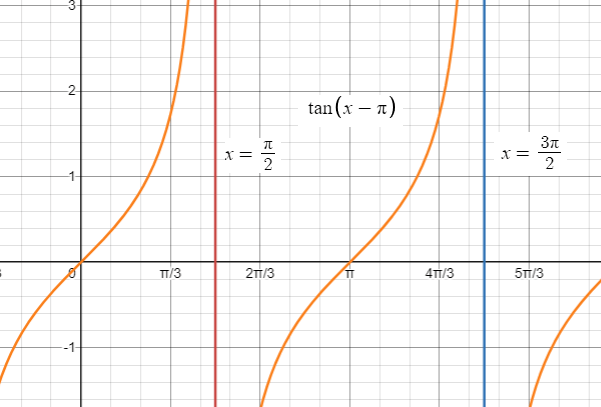
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling