FINDING VERTICAL ASYMPTOTES AND HOLES OF RATIONAL FUNCTIONS

Describe the vertical asymptotes and holes for the graph of each rational function.

Problem 1 :

Solution:

Vertical asymptotes:

Equate the denominator to zero and solve for x.

(x + 2) (x - 2) = 0

x + 2 = 0 and x - 2 = 0

x = -2 and x = 2

So, the vertical asymptotes are x = -2 and x = 2.

Holes:

The common factor found at both numerator and denominator is (x - 2).

Now, we have to make this common factor (x - 2) equal to zero.

x - 2 = 0

x = 2

So, there is a hole at x = 2.

Problem 2 :

Solution:

Vertical asymptotes:

Equate the denominator to zero and solve for x.

x(x - 1) = 0

x = 0 and x - 1 = 0

x = 0 and x = 1

So, the vertical asymptotes are x = 0 and x = 1.

Holes:

The common factor found at both numerator and denominator is x.

Now, we have to make this common factor x equal to zero.

x = 0

So, there is a hole at x = 0.

Problem 3 :

Vertical asymptotes:

Equate the denominator to zero and solve for x.

x² - 1 = 0

(x - 1)(x + 1) = 0

x - 1 = 0 and x + 1 = 0

x = 1 and x = -1

So, the vertical asymptotes are x = 1 and x = -1.

Holes:

After having factored, there is no common factor found at both numerator and denominator.

Hence, there is no hole for the given rational function.

Problem 4 :

Vertical asymptotes:

Equate the denominator to zero and solve for x.

x + 2 = 0

x = -2

So, the vertical asymptote is x = -2.

Holes:

In the given rational function, clearly there is no common factor found at both numerator and denominator.

So, there is no hole for the given rational function.

Problem 5 :

Solution: 

Vertical asymptotes:

Equate the denominator to zero and solve for x.

x² + 4 = 0

x² = -4

So, there is no asymptote.

Holes:

After having factored, there is no common factor found at both numerator and denominator.

Hence, there is no hole for the given rational function.

Problem 6 :

Solution:

Vertical asymptotes:

Equate the denominator to zero and solve for x.

x² - 9 = 0

(x + 3) (x - 3) = 0

x + 3 = 0 and x - 3 = 0

x = -3 and x = 3

So, the vertical asymptotes are x = -3 and x = 3.

Holes:

After having factored, the common factor found at both numerator and denominator is (x + 3).

Now, we have to make this common factor (x + 3) equal to zero.

x + 3 = 0

x = -3

So, there is a hole at x = -3.

Problem 7 :

Solution:

Vertical asymptotes:

Equate the denominator to zero and solve for x.

x - 4 = 0

x = 4

So, the vertical asymptote is x = 4.

Holes:

After having factored, there is no common factor found at both numerator and denominator.

Hence, there is no hole for the given rational function.

Problem 8 :

Solution:

Vertical asymptotes:

Equate the denominator to zero and solve for x.

So, the vertical asymptotes are x = -4/5 and x = 3.

Holes:

In the given rational function, clearly there is no common factor found at both numerator and denominator.

So, there is no hole for the given rational function.

Problem 9 :

Solution:

Vertical asymptotes:

Equate the denominator to zero and solve for x.

x² - 4 = 0

x² = 4

x = ±2

So, the vertical asymptotes are x = 2 and x = -2.

Holes: 

After having factored, there is no common factor found at both numerator and denominator.

Hence, there is no hole for the given rational function.

Problem 10 :

Suppose you start a home business typing technical research papers for college students. You must spend $3500 to replace your computer system. Then you estimate the cost of typing each page will be $0.02.

a. Write a rational function modeling your average cost per page. Graph the function.

b. How many pages must you type to bring your average cost per page to less than $1.50 per page, the amount you plan to charge?

Solution :

a.

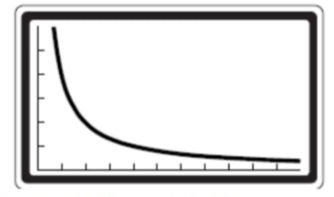
b. Average cost should be less than 1.50.