FINDING VERTEX OF DIFFERENT TYPES OF FUNCTIONS

The vertex is a point, that should be minimum or starting point of the curve or where the edges meet each other.

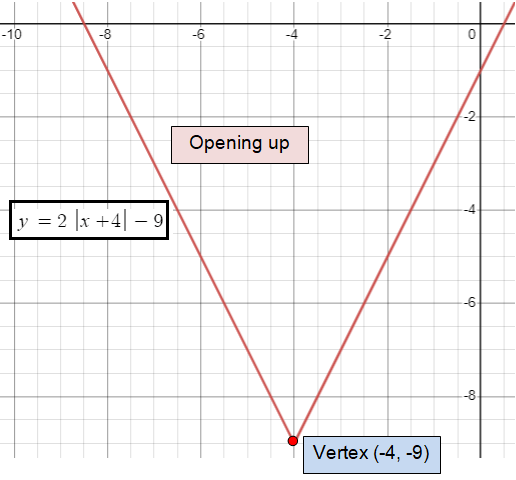
Vertex in absolute value function :

The general form of any absolute value function will be 

y = a |x - h| + k

Here (h, k) is the vertex of the absolute value function.

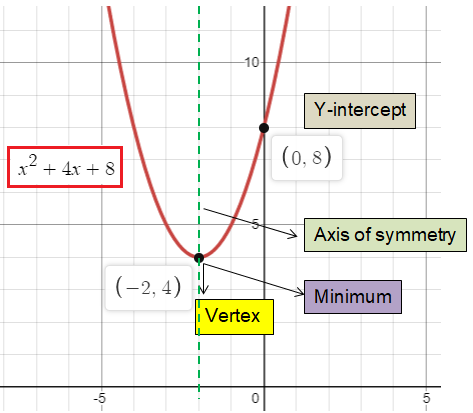
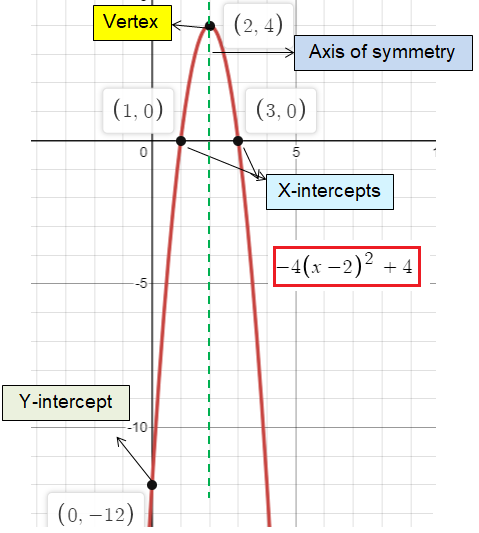
Vertex in quadratic function :

The general form of any quadratic function in vertex form will be 

y = a (x - h)² + k

Here (h, k) is the vertex of the quadratic function.

Vertex in square root function :

The general form of any square root function will be 

y = a√(x - h) + k

Here (h, k) is the vertex of the square root function.

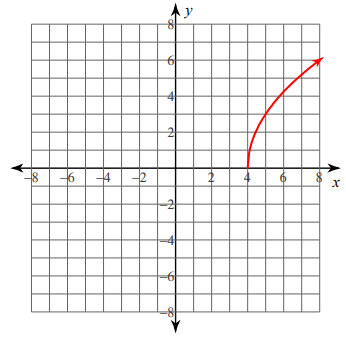
Vertex of the above square root function is at (4, 0).

Find the vertex practice: (all types)

Problem 1 :

y = √(x - 4) + 8 Vertex: (  ,  )

Solution:

y = √(x - 4) + 8

Type of given function :

Square root function.

General form of square root function :

y = √(x - h) + k

By comparing the above equation,

Vertex (h, k) = (4, 8)

The parent function y = √(x - 4) + 8 is shifted 4 units to the right from x = 0 and 8 unit up from y = 0.

Problem 2 :

y = -√x  Vertex: (  ,  )

Solution:

y = -√x

Type of given function :

Square root function.

General form of square root function :

y = √(x - h) + k

By comparing the above equation,

Vertex (h, k) = (0, 0)

Problem 3 :

y = -|x - 1|  Vertex: (  ,  )

Solution:

y = -|x - 1|

Type of given function :

Absolute value function.

General form of square root function :

y = a|(x - h)| + k

By comparing the above equation,

Vertex (h, k) = (1, 0)

Problem 4 :

y = √x - 7  Vertex: (  ,  )

Solution:

y = √x - 7

Type of given function :

Square root function.

General form of square root function :

y = √(x - h) + k

By comparing the above equation,

Vertex (h, k) = (0, -7)

Problem 5 :

Solution:

Type of given function :

Quadratic function.

General form of quadratic function :

y = a(x - h)² + k

By comparing the above equation,

Vertex (h, k) = (-10, 0)

Problem 6 :

y = 3√(x + 1)  Vertex: (  ,  )

Solution:

y = 3√(x + 1) 

Type of given function :

Square root function.

General form of square root function :

y = √(x - h) + k

By comparing the above equation,

Vertex (h, k) = (-1, 0)