FINDING UNKNOWN LENGTH BY PYTHAGOREAN THEOREM

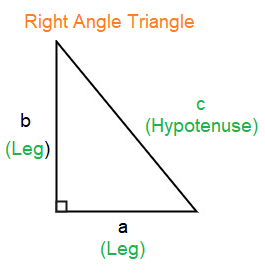
Pythagorean Theorem : 

In any right angled triangle, the length of square of hypotenuse is equal to the sum of the squares on the other two sides

In a right angled triangle, with hypotenuse c and legs a and b,

c² = a² + b²

Find the unknown lengths :

Problem 1 :

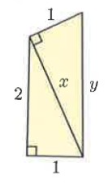
Solution :

In figure ∆ABC and ∆DAC.

AB = 2, BC = 1 and AC = x

DA = 1, AC = √5 and DC = y

Using Pythagoras theorem :

So, x = √5 and y = √6.

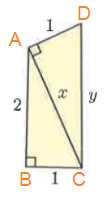
Problem 2 :

Solution :

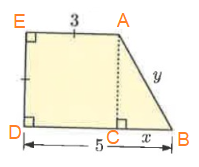
In figure BD = 5, AE = 3

 BC = BD - AE

BC = 5 - 3

BC = 2

In ∆ABC,

AC = 3, BC = 2 and AB = y

By using Pythagoras theorem,

AC² + BC² = AB²

3² + 2² = y²

9 + 4 = y²

y² = 13

y = √13

So, x = 2 and y = √13.

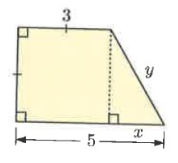
Problem 3 :

Solution :

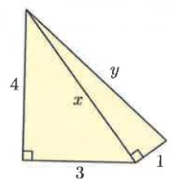
In figure ∆ABC and ∆ACD.

AB = 4, BC = 3 and AC = x

AC = 5, CD = 1 and AD = y

Using Pythagoras theorem :

So, x = 5 and y = √26.

Problem 4 :

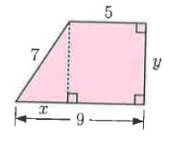
Solution :

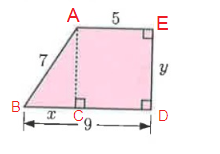
In figure BD = 9, AE = 5.

 BC = BD - AE

BC = 9 - 5

BC = 4

In figure ∆ABC

In ∆ABC,

AB = 7, BC = 4 and AC = y

By using Pythagoras theorem

AC² + BC² = AB²

 y² + 4² = 7²

y² + 16 = 49

y² = 49 - 16

y² = 33

y = √33

So, x = 4 and y = √33.

Problem 5 :

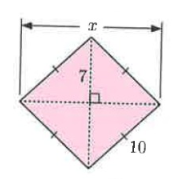
Solution:

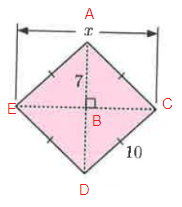
In figure ∆ABC.

In ∆ABC,

AB = 7, AC = 10 and BC = x

By using Pythagoras theorem,

AB² + BC² = AC²

7² + x² = 10²

x² = 100 - 49

x² = 51

x = √51

EC = 2x

x = 2√51

Problem 6 :

Solution :

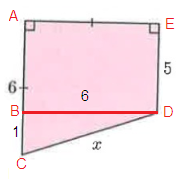
In figure ∆BCD.

In ∆BCD,

BC = 1, BD = 6 and CD = x

By using Pythagoras theorem

BC² + BD² = CD²

1² + 6² = x²

1 + 36 = x²

x² = 37

x = √37

Problem 7 :

Solution :

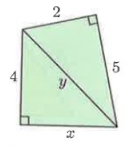
In figure ∆ABC and ∆ACD.

AD = 2, CD = 5 and AC = y

AB = 4, AC = √29 and BC = x

By using Pythagoras theorem,

So, x = √13 and y = √29.

Problem 8 :

Solution :

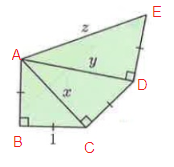
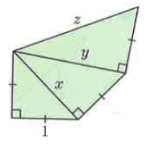
In figure ∆ABC, ∆ACD and ∆ADE.

AB = 1, BC = 1, AC = x, CD = 1, AD = y, DE = 1, and AE = z

By using Pythagoras theorem,

So, x = √2, y = √3 and z = 2.