FINDING THE VOLUME AND THE SURFACE AREA OF A SPHERE

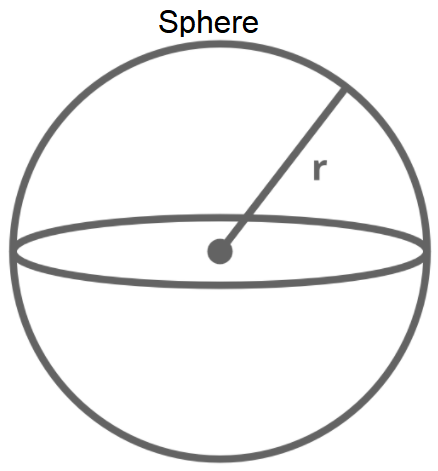
Formula for surface area of a sphere,

S = 4πr²

Formula for volume of a sphere 

V = (4/3)πr³

(where r is the radius of the sphere)

Find the surface area of the sphere. Round your answer to the nearest whole number.

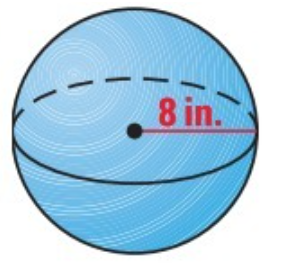
Problem 1 :

Solution :

Given, radius = 8 in

Formula for surface area of a sphere

S = 4πr²

Substitute π = 22/7 and r = 8

S = 4π (8)²

S = (4) (22/7) (64)

S = 804.57 in²

The surface area of the sphere is 804 in².

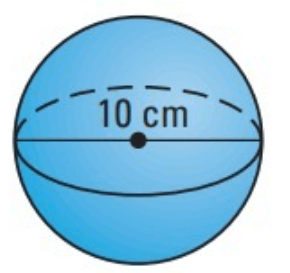
Problem 2 :

Solution :

Given, Diameter = 10cm.

Radius = d/2

               = 10/2

   Radius = 5 cm

Formula for surface area of a sphere,

S = 4πr²

Substitute π = 22/7 and r = 5

S = 4π (5)²

S = (4) (22/7) (25)

S = 314.28

The surface area of the sphere is 314 cm².

Find the volume of the sphere. Round your answer to the nearest whole number.

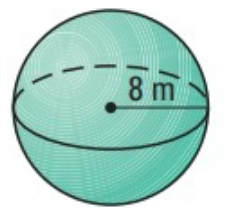
Problem 3 :

Solution :

Given, Radius = 8 m

Formula for volume of the sphere 

V = 4/3πr³

Substitute π = 22/7 and r = 8m

V = (4/3) ∙ (22/7) ∙ (8)³

V = (4/3) ∙ (22/7) ∙ 512

V = 2145 m³

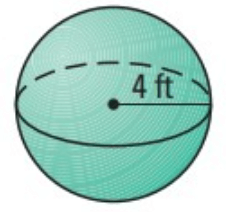
Problem 4 :

Solution :

Given, Radius = 4 ft

Formula for volume of the sphere 

V = 4/3 ∙ πr³

Substitute π = 22/7 and r = 4 ft

V = (4/3) ∙ (22/7) ∙ (4)³

V = (4/3) ∙ (22/7) ∙ 64

V = 268 ft³

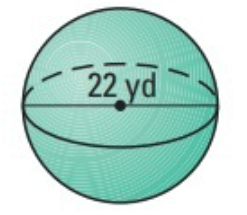
Problem 5 :

Solution :

Given, diameter = 22 yd

Radius = d/2

= 22/2

Radius = 11 yd

Formula for volume of the sphere 

V = 4/3 ∙ πr³

Substitute π = 22/7 and r = 11 yd

V = (4/3) ∙ (22/7) ∙ (11)³

V = (4/3) ∙ (22/7) ∙ (1331)

V = 5577 yd³

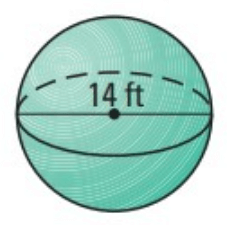
Problem 6 :

Solution :

Given, diameter = 14 ft

Radius = d/2

= 14/2

Radius = 7 ft

Formula for volume of the sphere 

V = 4/3 ∙ πr³

Substitute π = 22/7 and r = 7 ft

V = (4/3) ∙ (22/7) ∙ (7)³

V = (4/3) ∙ (22/7) ∙ (343)

V = 1437 ft³

Problem 7 :

The surface area of a sphere is 324π square centimeters. Find the volume of the sphere.

Solution :

Surface area of sphere = 324 π square centimeters

4πr² = 324π

r² = 324π / 4π

r² = 81

r = √81

r = 9

Volume of sphere = 4/3 ∙ πr³

= (4/3) ∙ π(9)³

= 972 π cm³

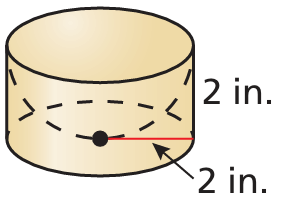
Problem 8 :

Find the volume of the composite solid.

Solution :

Radius = 2 inches and heigth = 2 inches

= Volume of cylinder - volume of hemisphere

= πr² h - (2/3) πr³

= πr²(h - 2r/3)

= 3.14(2)²(2 - 2(2)/3)

= 12.56 (2 - (4/3))

= 12.56 (6 - 4)/3

= 4.18(2)

= 8.37 cubic inches

Problem 9 :

Find the radius of a sphere with a surface area of 4π square feet.

Solution :

Surface area of sphere = 4π square feet

4πr² = 4π

r² = 1

r = 1

So, the radius of the sphere is 1 feet.

Problem 10 :

Find the radius of a sphere with a surface area of 1024π square inches.

Solution :

Surface area of sphere = 1024π square feet

4πr² = 1024π

r² = 1024π/4π

r² = 256

r = 16

So, the radius of the sphere is 16 inches

Problem 11 :

Find the diameter of a sphere with a surface area of 900π square meters.

Solution :

Surface area of sphere = 900π square meters.

4πr² = 900π

4r² = 900

r² = 900/4

r² = 225

r = 15

diameter = 2r ==> 2(15)

= 30 meter

So, the required diameter of the sphere is 30 meter.

Problem 12 :

Find the diameter of a sphere with a surface area of 196π square centimeters.

Solution :

Surface area of sphere = 196π square meters.

4πr² = 196π

4r² = 196

r² = 196/4

r² = 49

r = 7

Diameter = 2r ==> 2(7)

= 14 cm

So, the required diameter of the sphere is 14 cm.

Problem 13 :

You friend claims that if the radius of a sphere is doubled, then the surface area of the sphere will also be doubled. Is your friend correct? Explain your reasoning.

Solution :

Let r be the radius of the sphere

Surface area of sphere = 4πr²

When radius is doubled, then new radius will be 2r

Surface area of new sphere = 4π(2r)²

= 4π(4r²)

= 16πr²

= 4(4πr²)

= 4(Surface area of old sphere)

So, your's friend argument is incorrect.

Problem 14 :

A semicircle with a diameter of 18 inches is rotated about its diameter. Find the surface area and the volume of the solid formed.

Solution :

When rotating the shape semicircle, we get the shape hemisphere

Diameter of hemisphere = 18/2

= 9 inches

Surface area of hemisphere = 2πr²

= 2 x 22/7 x 9²

= 308 square inches

Volume  of hemisphere = (2/3)πr³

= (2/3) x 3.14 x 9³

= 16106.04 cubic inches

Problem 15 :

A silo has the dimensions shown. The top of the silo is a hemispherical shape. Find the volume of the silo.

Solution :

Volume of silo = volume of cylinder + volume of hemisphere

= πr² h + (2/3) πr³

radius (r) = 10 ft and height (h) = 60 ft

= π(10)² (60) + (2/3) π(10)³

= 6000π + (2000/3)π

= 6666.6π(approximately)