FINDING THE SLOPE FROM AN EQUATION

Find the slope of each line and decide the type of line 

(i) Raising   (ii) Falling   (iii)  Horizontal   (iv) Vertical

Problem 1 :

y = -5x - 1

Solution :

y = -5x - 1

The given equation is in slope intercept form. 

Comparing with y = mx + b

m = -5

Since the slope of negative, it is a falling line.

Problem 2 :

y = 1/3x - 4

Solution :

y = 1/3x – 4

The given equation is in slope intercept form. 

Comparing with y = mx + b

m = 1/3

Slope is 1/3. Since slope is positive, it is a raising line.

Problem 3 :

y = -1/5x - 4

Solution :

y = -1/5x - 4

It is in the slope intercept form y = mx + b

m = -1/5

Slope is -1/5. Since slope is negative, it is a falling line.

Problem 4 :

x = 1

Solution :

The given line is a vertical line, it will have undefined slope.

Problem 5 :

y = (1/4)x + 1

Solution :

y = (1/4)x + 1

The given equation is in slope intercept form. 

Comparing with y = mx + b

Slope (m) = 1/4

Since the slope is positive, it is raising line.

Problem 6 :

y = (-2/3)x - 1

Solution :

y = (-2/3)x - 1

The given equation is in slope intercept form. 

Slope (m) = -2/3

Since it has negative slope, it must be the falling line.

Problem 7 :

y = -x + 2

Solution :

y = -x + 2

Slope (m) = -1

Since it has negative slope, it must be a falling line.

Problem 8 :

y = -x - 1

Solution :

y = -x - 1

The given equation is in slope intercept form. 

Slope (m) = -1

Since it has negative slope, it must be the falling line.

Problem 9 :

2x + 3y = 9

Solution :

Given, 2x + 3y = 9

The given equation is in standard form, to find slope we have to convert it into slope intercept form (y = mx +b)

 3y = -2x + 9

y = -2x/3 + 9/3

y = (-2/3)x + 3

Comparing with y = mx + b

m = -2/3

Since it has negative slope, it must be a falling line.

Problem 10 :

5x + 2y = 6

Solution :

 5x + 2y = 6

Converting into slope intercept form, we get

 2y = -5x + 6

y = -5x/2 + 6/2

y = (-5/2)x + 3

Comparing with y = mx + b

m = -5/2

Since it has negative slope, it must be the falling line.

Problem 11 :

The equation 

y = 1.5x + 35

represents the cost y (in dollars) of the family meal when the food costs $35 and x beverages are purchased.

a. Graph the equation.

b. Use the graph to estimate the cost of the family meal when 5 beverages are purchased.

c. Use the equation to find the exact cost of the family meal when 5 beverages are purchased.

Solution :

y = 1.5x + 35

Comparing the given equation with y = mx + b, we get m = 1.5

Converting the decimal into fraction, we get

m = 15/10

m = 3/2

a)

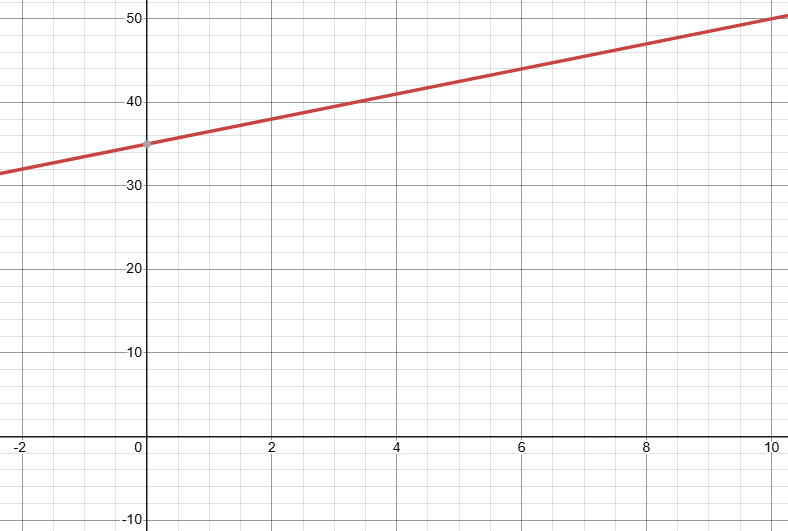
b)