FINDING THE MISSING SIDES AND ANGLES USING LAW OF SINES

Problem 1 :

Find AC

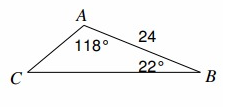
Solution :

CB = a, AB = c = 24, AC = b

∠̇A = 118º, ∠̇B = 22^º, 

In triangle ABC, 

∠̇A + ∠̇B + ∠̇C = 180^º

118^º + 22^º + ∠̇C = 180^º

140^º + ∠̇C = 180^º

∠̇C = 180^º - 140^º

∠̇C = 40^º

So, the missing side and missing angle are 14 and 40 degree.

Problem 2 :

Find AB

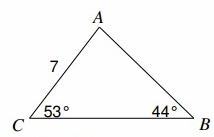
Solution :

CB = a, AC = b = 7, AB = c

∠̇B = 44^º, ∠̇C = 53^º, 

In triangle ABC, 

∠̇A + ∠̇B + ∠̇C = 180^º

∠̇A + 44^º + 53^º = 180^º

∠̇A + 97^º = 180^º

∠̇A = 180^º - 97^º

∠̇A = 83^º

So, the missing side and missing angle are 8 and 83 degree.

Problem 3 :

Find BC

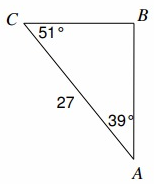
Solution :

CB = a, AC = b = 27, AB = c

∠̇A = 39^º, ∠̇C = 51^º, 

In triangle ABC, 

∠̇A + ∠̇B + ∠̇C = 180^º

∠̇39^º + ∠̇B + 51^º = 180^º

∠̇B + 90^º = 180^º

∠̇B = 180^º - 90^º

∠̇B = 90^º

So, the missing side and missing angle are 17 and 90 degree.

Problem 4 :

Find AB

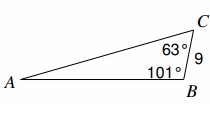
Solution :

CB = a = 9, AC = b, AB = c

∠̇B = 101º, ∠̇C = 63º, 

In triangle ABC, 

∠̇A + ∠̇B + ∠̇C = 180º

∠̇A + 101º + 63º = 180º

∠̇A + 164º = 180º

∠̇A = 180º - 164º

∠̇A = 16º

So, the missing side and missing angle are 29.1 and 16 degree.

Problem 5 :

Find BC

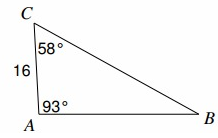
Solution :

CB = a, AC = b = 16, AB = c

∠̇A = 93^º, ∠̇C = 58^º, 

In triangle ABC, 

∠̇A + ∠̇B + ∠̇C = 180^º

93^º + ∠̇B  + 58^º = 180^º

∠̇B + 151^º = 180^º

∠̇B = 180^º - 151^º

∠̇B = 29^º

So, the missing side and missing angle are 33 and 29 degree.

Problem 6 :

Find m∠̇C

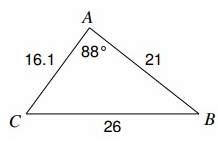
Solution :

CB = a = 26, AC = b = 16.1, AB = c = 21

∠̇A = 88^º 

Hence, the required angle is m∠̇C = 54^º.

Problem 7 :

Find m∠̇C

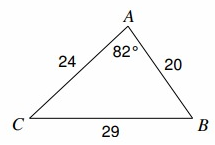
Solution :

CB = a = 29, AC = b = 24, AB = c = 20

∠̇A = 82^º 

Hence, the required angle is m∠̇C = 43.1^º.

Problem 8 :

Find m∠̇C

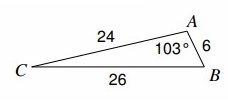
Solution :

CB = a = 26, AC = b = 24, AB = c = 6

∠̇A = 103^º 

Hence, the required angle is m∠̇C = 13^º.

Problem 9 :

Find m∠̇A

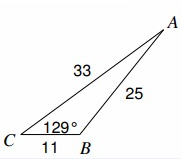
Solution :

CB = a = 11, AC = b = 33, AB = c = 25

∠̇B = 129^º 

Hence, the required angle is m∠̇A = 15^º.

Problem 10 :

Find m∠̇C

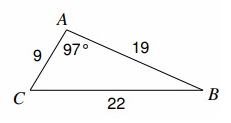
Solution :

CB = a = 22, AC = b = 9, AB = c = 19

∠̇A = 97^º 

Hence, the required angle is m∠̇C = 59^º.