FINDING THE MISSING DIAGONAL OF A RHOMBUS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
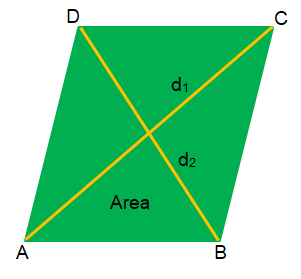
In the above figure, ABCD is a rhombus.
Formula for the Area of the Rhombus,
Area = 1/2 × d1 × d2
(Where d1 and d2 are the diagonals of the rhombus)
In figure, AC = d1 and BD = d2
Area = 1/2 × AC × BD
Find the length of the missing diagonal in each rhombus.
Problem 1 :
If WY = 70 yd, find XZ.
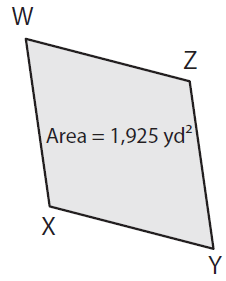
Solution :
Given, Area = 1925 yd² and WY = 70 yd
Area of the rhombus = 1/2 × d1 × d2
Here d1 = WY and d2 = XZ
Area = 1/2 × WY × XZ
1925 yd² = 1/2 × 70 yd × d2
1925 yd² = 35 yd × d2
(1925 yd²) / 35 yd = d2
XZ = d2 = 55 yd
Problem 2 :
If FH = 6 ft, find EG.
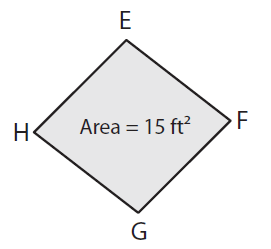
Solution :
Given, Area = 15 ft² and FH = 6 ft
Area of the rhombus = 1/2 × d1 × d2
Here FH = d1 and EG = d2
Area = 1/2 × FH × EG
15 ft² = 1/2 × 6 ft × d2
15 ft² = 3 ft × d2
(15 ft²) / 3 ft = d2
EG = d2 = 5 ft
Problem 3 :
If KM = 35 in, find LN.
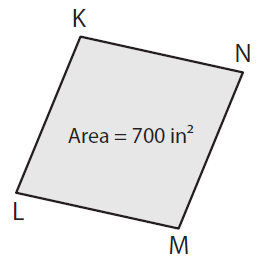
Solution :
Given, Area = 700 in² and KM = 35 in
Area of the rhombus = 1/2 × d1 × d2
Here d1 = KM and d2 = LN
Area = 1/2 × KM × LN
700 in² = 1/2 × 35 in × d2
(700 in² × 2) / 35 in = d2
(1400 in²) / 35 in = d2
LN = d2 = 40 in
Problem 4 :
If VT = 7ft, find SU.
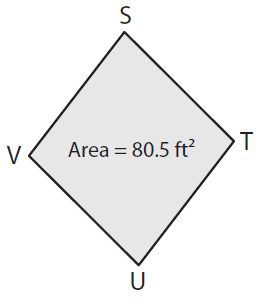
Solution :
Given, Area = 80.5 ft² and VT = 7 ft
Area of the rhombus = 1/2 × d1 × d2
Here d1 = VT and d2 = SU
Area = 1/2 × VT × SU
80.5 ft² = 1/2 × 7 ft × d2
(80. 5 ft² × 2) / 7 ft = d2
d2 = (161 ft²) / 7 ft
SU = d2 = 23 ft
Problem 5 :
If BD = 16 in, find AC.
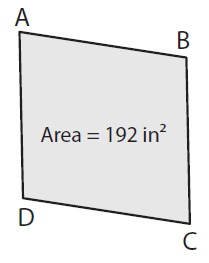
Solution :
Given, Area = 192 in² and BD = 16 in
Area of the rhombus = 1/2 × d1 × d2
Here d1 = BD and d2 = AC
Area = 1/2 × BD × AC
192 in² = 1/2 × 16 in × d2
192 in² = 8 in × d2
d2 = (192 in²) / 8 in
AC = d2 = 24 in
Problem 6 :
If VX = 49 yd, find UW.
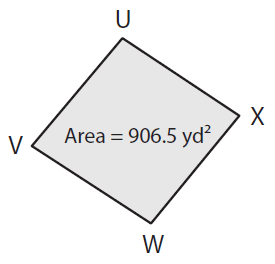
Solution :
Given, Area = 906.5 yd² and VX = 49 yd
Area of the rhombus = 1/2 × d1 × d2
Here d1 = VX and d2 = UW
Area = 1/2 × VX × UW
906.5 yd² = 1/2 × 49 yd × d2
(906.5 yd² × 2) / 49 yd = d2
(1813 yd²) / 49 yd = d2
UW = d2 = 37 yd
Problem 7 :
The length of one of the diagonal of a rhombus is 38 inches. Find the length of the other diagonal, if the area is 646 square inches.
Solution :
Given, Area = 646 square inches
Length of one diagonal d1 = 38 inches
Length of other diagonal d2 = ?
Area of the rhombus = 1/2 × d1 × d2
646 in² = 1/2 × 38 in × d2
646 in² = 19 in × d2
(646 in²) / 19 in = d2
d2 = 34 inches
So, the length of other diagonal of a rhombus is 34 in.
Problem 8 :
The area of a rhombus is 125 square yards. If one of the diagonals measures 10 yards, find the length of the other diagonal.
Solution :
Given, Area = 125 square yards
Length of one diagonal d1 = 10 yards
Length of other diagonal d2 = ?
Area of the rhombus = 1/2 × d1 × d2
125 yd² = 1/2 × 10 yd × d2
125 yd² = 5 yd × d2
(125 yd²) / 5 yd = d2
d2 = 25 yd
So, the length of other diagonal of a rhombus is 25 yd.
Problem 9 :
Find the area of the kite or rhombus.
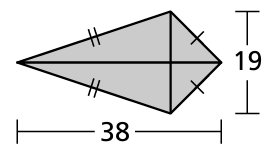
Solution :
Length of diagonals are 38 and 19
Area of kite or rhombus = (1/2) x d1 x d2
= (1/2) x 38 x 19
= 19 x 19
= 361 square units.
Problem 10 :
Find the area of the kite or rhombus.
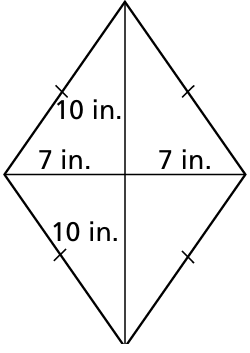
Solution :
Length of diagonal 1 = 7 + 7 ==> 14 inches
Length of diagonal 2 = 10 + 10 ==> 20 inches
Area of rhombus = (1/2) x 14 x 20
= 7 x 20
= 140 square inches
Problem 11 :
Find the area of the kite or rhombus.
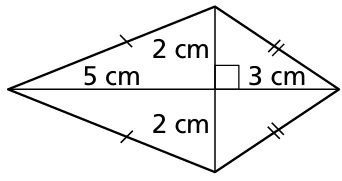
Solution :
Length of diagonal 1 = 5 + 3 ==> 8 cm
Length of diagonal 2 = 2 + 2 ==> 4 cm
Area of rhombus = (1/2) x 8 x 4
= 4 x 4
= 16 cm2
Problem 12 :
Find the area of the kite or rhombus.
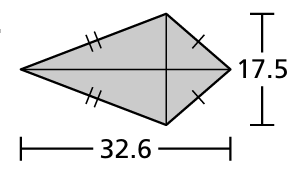
Solution :
Length of diagonal 1 = 32.6 inches
Length of diagonal 2 = 17.5 inches
Area of kite = (1/2) x 32.6 x 17.5
= 16.3 x 17.5
= 285.25 square inches.
Problem 13 :
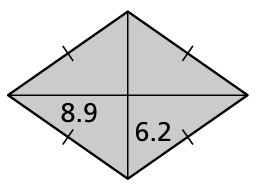
Solution :
Length of diagonal 1 = 8.9 + 8.9
= 17.8
Length of diagonal 2 = 6.2 + 6.2
= 12.4
Area of kite = (1/2) x 12.4 x 17.8
= 6.2 x 17.8
= 110.36 square inches.
Problem 14 :
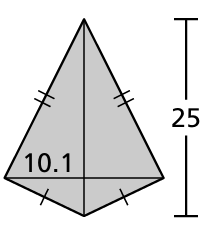
Solution :
Length of diagonal 1 = 25
Length of diagonal 2 = 10.1 + 10.1
= 20.2
Area of kite = (1/2) x 20.2 x 25
= 10.1 x 25
= 252.5 square inches
= 110.36 square inches.
Problem 15 :
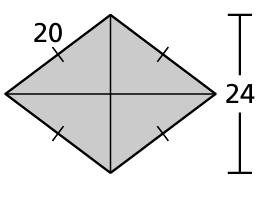
Solution :
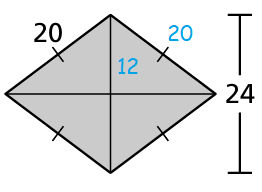
In the triangle above, the base of the triangle be x.
202 = 122 + x2
400 = 144 + x2
x2 = 400 - 144
x2 = 256
x = 16
Length of diagonal 1 = 24
length of diagonal 2 = 16 + 16 ==> 32
Area of rhombus = (1/2) x 24 x 32
= 12 x 32
= 384 square units.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling