FINDING THE MISSING DIAGONAL OF A KITE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
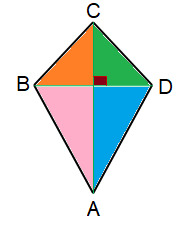
In the above figure, ABCD is a Kite.
Formula for the Area of a Kite,
Area = 1/2 × d1 × d2
(Where d1 and d2 are the diagonals of the rhombus)
In figure, AC = d1 and BD = d2
Area = 1/2 × AC × BD
Find the length of the missing diagonal in each kite.
Problem 1 :
Find TR if QS = 24 ft.
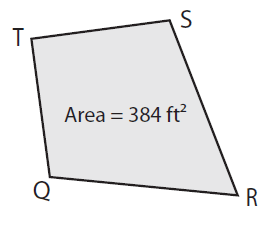
Solution:
Given, Area = 384 ft² and QS = 24 ft
Area of kite = 1/2 × d1 × d2
Here d1 = QS and d2 = TR
Area = 1/2 × QS × TR
384 ft² = 1/2 × 24 ft × d2
(384 ft²) = 12 ft × d2
(384 ft²) / 12 ft = d2
TR = d2 = 32 ft
So, the length of other diagonal of a kite TR is 32 ft.
Problem 2 :
Find VX if WU = 28 in.
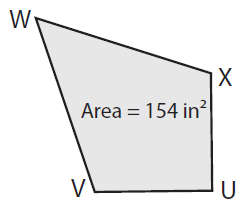
Solution :
Given, Area = 154 in² and WU = 28 in
Area of kite = 1/2 × d1 × d2
Here d1 = WU and d2 = VX
Area = 1/2 × WU × VX
154 in² = 1/2 × 28 in × d2
(154 in²) = 14 in × d2
(154 in²) / 14 in = d2
VX = d2 = 11 in
So, the length of other diagonal of a kite VX is 11 in.
Problem 3 :
Find HF if GE = 43 yd.
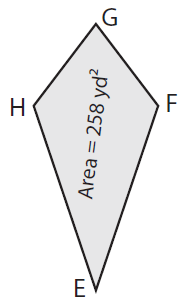
Solution :
Given, Area = 258 yd² and GE = 43 yd
Area of kite = 1/2 × d1 × d2
Here d1 = GE and d2 = HF
Area = 1/2 × GE × HF
258 yd² = 1/2 × 43 yd × d2
(258 yd² × 2) = 43 yd × d2
(516 yd²) / (43 yd) = d2
HF = d2 = 12 yd
So, the length of other diagonal of a kite HF is 12 yd.
Problem 4 :
Find NL if MK = 18 in.
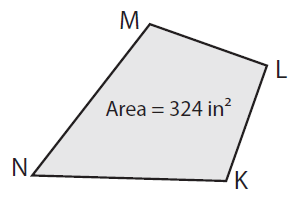
Solution :
Given, Area = 324 in² and MK = 18 in
Area of kite = 1/2 × d1 × d2
Here d1 = MK and d2 = NL
Area = 1/2 × MK × NL
324 in² = 1/2 × 18 in × d2
(324 in²) = 9 in × d2
(324 in²) / 9 in = d2
NL = d2 = 36 in
So, the length of other diagonal of a kite NL is 36 in.
Problem 5 :
Find BD if AC = 47 yd.
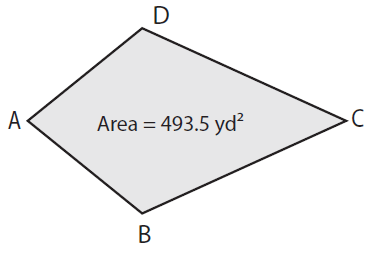
Solution :
Given, Area = 493.5 yd² and AC = 47 yd
Area of kite = 1/2 × d1 × d2
Here d1 = AC and d2 = BD
Area = 1/2 × AC × BD
493.5 yd² = 1/2 × 47 yd × d2
(493.5 yd² × 2) = 47 yd × d2
(987 yd²) / (47 yd) = d2
BD = d2 = 21 yd
So, the length of other diagonal of a kite BD is 21 yd.
Problem 6 :
Find TV if SU = 30 ft.
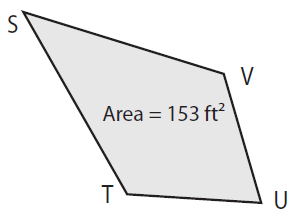
Solution :
Given, Area = 153 ft² and SU = 30 ft
Area of kite = 1/2 × d1 × d2
Here d1 = SU and d2 = TV
Area = 1/2 × SU × TV
153 ft² = 30 ft × d2 / 2
(153 ft²) = 15 ft × d2
(153 ft²) / 15 ft = d2
TV = d2 = 10.2 ft
So, the length of other diagonal of a kite TV is 10.2 ft.
Problem 7 :
Find EG if DF = 15 ft.
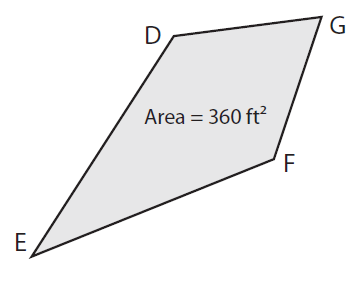
Solution :
Given, Area = 360 ft² and DF = 15 ft
Area of kite = 1/2 × d1 × d2
Here d1 = DF and d2 = EG
Area = 1/2 × DF × EG
360 ft² = 15 ft × d2 / 2
(360 ft² × 2) / 15 ft = d2
(720 ft²) / 15 ft = d2
EG = d2 = 48 ft
So, the length of other diagonal of a kite EG is 48 ft.
Problem 8 :
Find XZ if WY = 32 in.
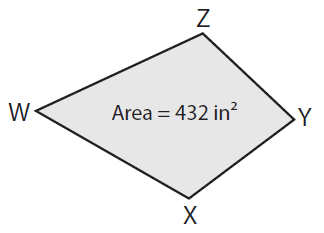
Solution :
Given, Area = 432 in² and WY = 32 in
Area of kite = 1/2 × d1 × d2
Here d1 = WY and d2 = XZ
Area = 1/2 × WY × XZ
432 in² = 1/2 × 32 in × d2
(432 in²) = 16 in × d2
(432 in²) / 16 in = d2
XZ = d2 = 27 in
So, the length of other diagonal of a kite XZ is 27 in.
Problem 9 :
Find QS if PR = 11 yd.
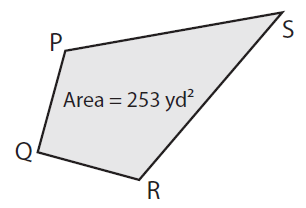
Solution :
Given, Area = 253 yd² and PR = 11 yd
Area of kite = 1/2 × d1 × d2
Here d1 = PR and d2 = QS
Area = 1/2 × PR × QS
253 yd² = 1/2 × 11 yd × d2
(253 yd² × 2) = 11 yd × d2
(506 yd²) / (11 yd) = d2
QS = d2 = 46 yd
So, the length of other diagonal of a kite QS is 46 yd.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling