FINDING THE MEAN MEDIAN AND MODE FROM A FREQUENCY TABLE

Problem 1 :

Each student in a class of 20 students is assigned a number between 1 and 10 to indicate his or her fitness.

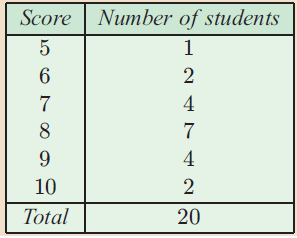
Calculate the

a) mean      b) Median         c) Mode       d) Range

Solution :

a)  Mean :

Mean = Sum of all values / Total number of values

= [5(1) + 6(2) + 7(4) + 8(7) + 9(4) + 10(2)] / 20

= (5 + 12 + 28 + 56 + 36 + 20)/20

= 157/20

= 7.85

So, the required mean is 7.85.

b) Median :

N = 20 (even)

Average of N/2 ^th element + (N/2) + 1 ^th element = median

= 10^th + 11^th elements

10^th and 11^th elements are 8.

Median = (8 + 8)/2

= 8

c) Mode :

The highest frequency is 7, its corresponding score is 8. So, mode = 8.

Range :

Least score = 5, highest score = 10

Range = 10 - 5

= 5

Problem 2 :

The members of a school band were each asked how many musical instruments they played. The results were 

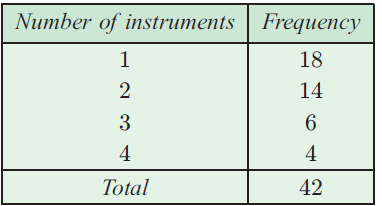
Calculate the

a) mean      b) Median         c) Mode       d) Range

Solution :

a)  Mean :

Mean = Sum of all values / Total number of values

= [1(18) + 2(14) + 3(6) + 4(4)] / 42

= (18 + 28 + 18 + 16) / 42

= 80/42

= 1.90

b)  Median :

N = 42 (even)

Average of N/2 ^th element + (N/2) + 1 ^th element = median

= 21^th + 22^th elements

= (2+2)/2

= 2 is the median

c) Mode :

The highest frequency is 1, its corresponding score is 18. So, mode = 18.

Range :

Least number of instruments = 1, highest number of instruments = 4

Range = 4 - 1

= 3

Problem 3 :

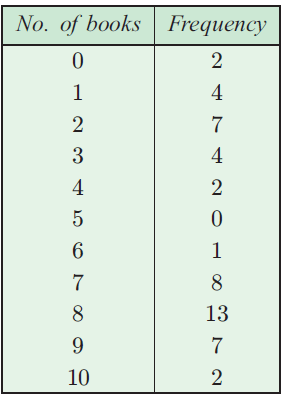
The following frequency table records the number of books read in the last year by 50 fifteen years old.

a)  For this data, find the 

a) mean      b) Median         c) Mode       d) Range

b) Construct a vertical bar chart for the data and show the position of the measures of center on the horizontal axis.

c) Describe the distribution of the data

d)  Why is the mean smaller than the median for this data ?

e) Which measure of center would be most suitable for this data set ?

Solution :

a) mean

= (0 + 4 + 14 + 12 + 8 + 0 + 6 + 56 + 104 + 63 + 20) / 50

= 287/50

= 5.74

b) Median :

Total number of terms (N) = 50

Median = (25^th + 26^th)  terms / 2

By creating frequency table, we get these elements simply.

25^th element = 7, 26^th element = 7

= (7 + 7)/2

= 7 is the median

c) Mode :

The highest frequency is 13, so mode is 8.

d) Range :

= 10 - 0

= 10

b) Constructing vertical bar :

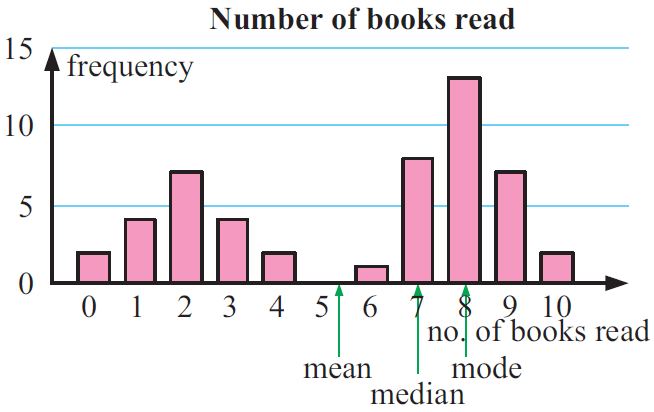
d)  The mean takes into account the full range of numbers of books read and is affected by extreme values. Also the values which are lower than the median are well below it.

e) Median.

Problem 4 :

Hui breeds ducks. The number of ducking survying for each pair after one month is recorded in the table,

a) Calculate the

i) Mean       ii) Median      iii) Mode      iv) Range

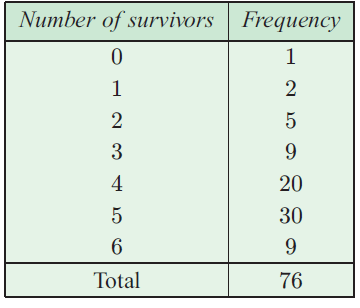
b) Is the data skewed

c)  How does the skewness of the data affect the measures of the middle of the distribution?

Solution :

a) i) Mean

= [0(1) + 1(2) + 2(5) + 3(9) + 4(20) + 5(30) + 6(9)]/76

= (0 + 2 + 10 + 27 + 80 + 150 + 54)/76

= 323/76

= 4.25

ii) Median

N = 76, N/2 ==> 38

Median = (5 + 5)/2

= 5

iii) Mode = 5 is repeating 30 times. So, mode = 5

iv) Range :

= 6 - 0

= 6

b)  The mean is negatively skewed

c) The mean is less than the mode and median.