FINDING THE DOMAIN AND RANGE OF AN EXPONENTIAL FUNCTION

Exponential function will be in any of the following forms.

y = b^x

(or)

y = ab^x

(or)

y = ab^x-h + k

Domain :

Domain of exponential function is all real values. (-∞, ∞).

Range :

(k, ∞) or (-∞, k) can be any one of them, based on exponential growth or decay can be decided.

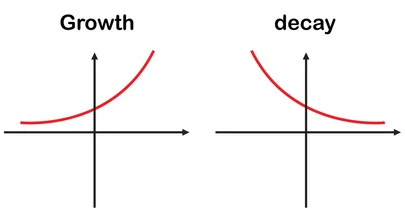
Exponential growth or decay :

If b > 0 for growth and 0 < b < 1 when it is decay.

Horizontal asymptotes :

The exponential function which is in the form

y = ab^x-h + k

x = k is the horizontal asymptote.

Find:

1) Domain

2) Range

3) Exponential growth or decay

4) Horizontal asymptote

Problem 1 :

f(x) = 3^x

Solution:

Domain:

The domain is all real number.

(-∞, ∞)

Range:

The range is all positive real numbers.

(0, ∞)

Exponential growth or decay:

f(x) = 3^x

if x = -3, f(x) = 3^-3 = 1/27

if x = -2, f(x) = 3^-2 = 1/9

if x = -1, f(x) = 3^-1 = 1/3

if x = 0, f(x) = 3⁰ = 1

if x = 1, f(x) = 3¹ = 3

Since the multiplication factor(b) is 3 > 1, this is an exponential growth function.

Horizontal asymptote:

y = 0

Problem 2 :

f(x) = -(3^x)

Solution:

Domain:

The domain is all real number.

(-∞, ∞)

Range:

The range is all negative real numbers.

(-∞, 0)

Exponential growth or decay:

f(x) = -(3^x)

a = -1, b = 3 > 3

if x = -3, f(x) = -(3^-3) = -1/27

if x = -2, f(x) = -(3^-2) = -1/9

if x = -1, f(x) = -(3^-1) = -1/3

if x = 0, f(x) = -(3⁰) = -1

if x = 1, f(x) = -(3¹) = -3

Multiplication factor is 3, but we have negative. Then, it is reflection.

Horizontal asymptote:

y = 0

Problem 3 :

f(x) = 3^-x

Solution:

Domain:

The domain is all real number.

(-∞, ∞)

Range:

The range is all positive real numbers.

(0, ∞)

Exponential growth or decay:

f(x) = 3^-x

if x = -3, f(x) = 3^-(-3) = 27

if x = -2, f(x) = 3^-(-2) = 9

if x = -1, f(x) = 3^-(-1) = 3

if x = 0, f(x) = 3⁰ = 1

if x = 1, f(x) = 3^-(1) = 1/3

This is an exponential decay.

Horizontal asymptote:

y = 0

Problem 4 :

f(x) = (1/3)^x

Solution:

Domain:

The domain is all real number.

(-∞, ∞)

Range:

The range is all positive real numbers.

(0, ∞)

Exponential growth or decay:

a = 1, b = 1/3 < 1

f(x) = (1/3)^x

if x = -3, f(x) = (1/3)^-3 = 27

if x = -2, f(x) = (1/3)^-2 = 9

if x = -1, f(x) = (1/3)^-1 = 3 

if x = 0, f(x) = (1/3)⁰ = 1

if x = 1, f(x) = (1/3)¹ = 1/3

This is an exponential decay function.

Horizontal asymptote:

y = 0

Problem 5 :

f(x) = 2^x - 3

Solution:

Domain:

The domain is all real number.

(-∞, ∞)

Range:

(-3, ∞)

Exponential growth or decay:

a = 1, b = 2 > 1

if x = -3, f(x) = 2^-3 - 3 = (1/8) - 3 = -2.875

if x = -2, f(x) = 2^-2 - 3 = (1/4) - 3 = -2.75

if x = -1, f(x) = 2^-1 - 3 = (1/2) - 3 = -2.5

if x = 0, f(x) = 2⁰ - 3 = 1 - 3 = -2

if x = 1, f(x) = 2¹ - 3 = 2 - 3 = -1

if x = 2, f(x) = 2² - 3 = 4 - 3 = 1

This is exponential growth function.

Horizontal asymptote:

y = -3

Problem 6 :

f(x) = 2^x-3

Solution:

Domain:

The domain is all real number.

(-∞, ∞)

Range:

(0, ∞)

Exponential growth or decay:

if x = -2, f(x) = 2^-2-3 = 2^-5 = 1/32

if x = -1, f(x) = 2^-1-3 = 2^-4 = 1/16

if x = 1, f(x) = 2^1-3 = 2^-2 = 1/4       

if x = 2, f(x) = 2^2-3 = 2^-1 = 1/2     

This is an exponential growth function.

Horizontal asymptote:

y = 0

Problem 7 :

f(x) = 2^x+5 - 5

Solution:

Domain:

The domain is all real number.

(-∞, ∞)

Range:

(-5, ∞)

Exponential growth or decay:

if x = -2, f(x) = 2^-2+5 - 5 = 2³ - 5 = 3 

if x = -1, f(x) = 2^-1+5 - 5 = 2⁴- 5 = 11

if x = 0, f(x) = 2⁰⁺⁵ - 5 = 2⁵ - 5 = 27

if x = 1, f(x) = 2¹⁺⁵ - 5 = 2⁶ - 5 = 59

This is an exponential growth function.

Horizontal asymptote:

y = -5

Problem 8 :

f(x) = -2^-x

Solution:

Domain:

The domain is all real number.

(-∞, ∞)

Range:

(-∞, 0)

Exponential growth or decay:

if x = -2, f(x) = -2^-(-2) = -2² = -4

if x = -1, f(x) = -2^-(-1) = -2¹ = -2

if x = 0, f(x) = -2⁽⁰⁾ = -1

if x = 1, f(x) = -2^-1 = -1/2

if x = 2, f(x) = -2^-2 = -1/4

This is an exponential growth function.

Horizontal asymptote:

y = 0

Problem 9 :

f(x) = -2^x+3 + 1

Solution:                         

Domain:

The domain is all real number.

(-∞, ∞)

Range:

(-∞, 1)

Exponential growth or decay:

if x = -2, f(x) = -2^-2+3 + 1 = -2 + 1 = -1

if x = -1, f(x) = -2^-1+3 + 1 = -4 + 1 = -3

if x = 0, f(x) = -2⁰⁺³ + 1 = -8 + 1 = -7

if x = 1, f(x) = -2¹⁺³ + 1 = -16 + 1 = -15

if x = 2, f(x) = -2²⁺³ + 1 = -32 + 1 = -31

This is an exponential decay function.

Horizontal asymptote:

y = 1

Problem 10 :

f(x) = (1/2)^x-3 - 4

Solution:

Domain:

The domain is all real number.

(-∞, ∞)

Range:

(-4, ∞)

Exponential growth or decay:

if x = -2, f(x) = (1/2)^-2-3 - 4 = 32 - 4 = 28

if x = -1, f(x) = (1/2)^-1-3 - 4 = 16 - 4 = 12

if x = 0, f(x) = (1/2)^0-3 - 4 =8 - 4 = 4

if x = 1, f(x) = (1/2)^1-3 - 4 = 4 - 4 = 0

if x = 2, f(x) = (1/2)^2-3 - 4 = 2 - 4 = -2

This is an exponential decay function.

Horizontal asymptote:

y = -4