FINDING THE ANGLE RELATIONSHIP IN PARALLEL LINES AND TRANSVERSAL

Angles Pairs in Parallel Lines Cut by a Transversal

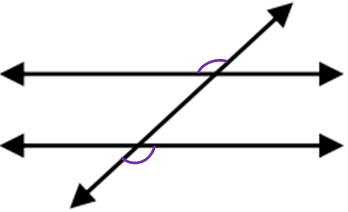
Corresponding Angles:

Corresponding Angles that lie on the same side of the transversal and on the same side of the parallel lines. These angles are in the same "corner" and are congruent.

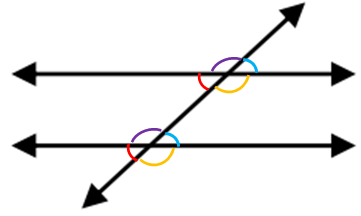
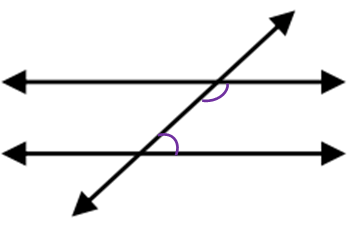
Alternate Interior Angles:

Alternate Interior Angles on opposite sides of the transversal and inside the two parallel lines. These angles are congruent.

Alternate Exterior Angles:

Alternate Exterior Angles on opposite sides of the transversal and outside the two parallel lines. These angles are congruent.

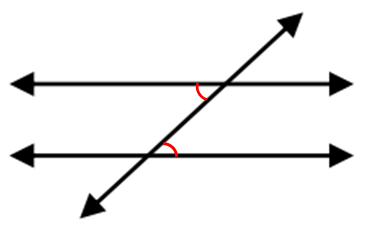
Same-Side Interior:

Same-Side Interior on the same side of the transversal and inside the parallel lines. These angles are supplementary.

Same-Side Exterior:

Same-Side Exterior on the same side of the transversal and outside the parallel lines. These angles are supplementary.

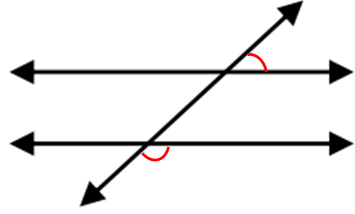
Vertical Angles:

Vertical Angles that are across from each other and are formed by any intersecting lines (not just parallel lines and transversal). These angles are supplementary.

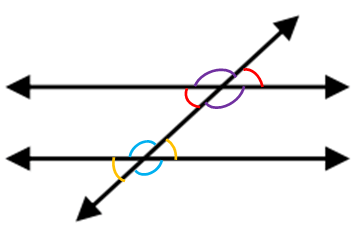
For each set of angles name the angle pair and find the missing measurements.

Problem 1 :

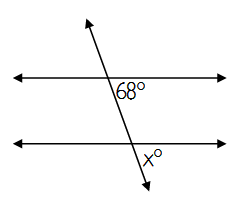
Type of angle pair ______

These angles are ______

So, x = _____

Solution:

Type of angle pair Corresponding

These angles are Congruent

So, x = 68°

Problem 2 :

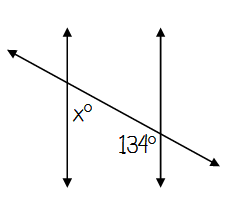
Type of angle pair _____

These angles angles are _____

So, x = ____

Solution:

Type of angle pair Same-Side Interior

These angles angles are Supplementary

So, x = 46°

Problem 3 :

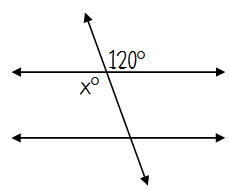
Type of angle pair _____

These angles are _____

So, x = ___

Solution:

Type of angle pair Vertical

These angles are Congruent

So, x = 120°

Problem 4 :

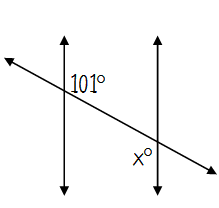
Type of angle pair ____

These angles are _____

So, x = ____

Solution:

Type of angle pair Alternate Interior

These angles are Congruent

So, x = 101°

Problem 5 :

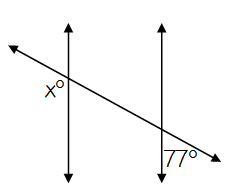
Type of angle pair ____

These angles are _____

So, x = ___

Solution:

Type of angle pair Same-Side Exterior

These angles are Supplementary

So, x = 103°

Problem 6 :

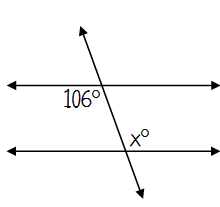
Type of angle pair _____

These angles are ____

So, x = ____

Solution:

Type of angle pair Alternate Interior 

These angles are Congruent

So, x = 106°

Problem 7 :

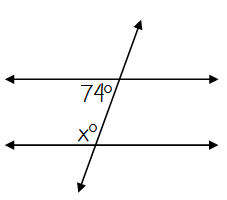
Type of angle pair _____

These angles are ____

So, x = ____

Solution:

Type of angle pair Same-Side Interior

These angles are Supplementary

So, x = 106°

Problem 8 :

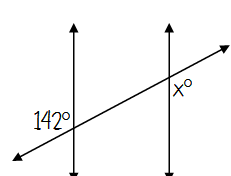
Type of angle pair _____

These angles are ____

So, x = ____

Solution:

Type of angle pair Alternate Interior

These angles are Congruent

So, x = 142°

For each set of angles name the angle pair, write the equation, solve the equation for x, and plug in x to find the missing angle measurements.

Problem 9 :

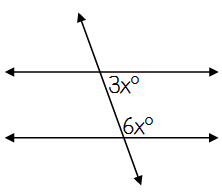
Type of angle pair ____

These angles are ____

Equation ____

x = ____

Angle Measurements = ____

Solution:

Type of angle pair Same-Side Interior

These angles are Supplementary

Equation 3x + 6x = 180

9x = 180

x = 20

Angle Measurements = 60° & 120°

Problem 10 :

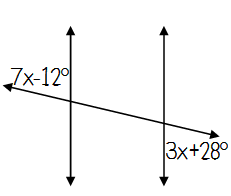
Type of angle pair ____

These angles are ____

Equation ____

x = ____

Angle Measurements = ____

Solution:

Type of angle pair Alternate Exterior

These angles are Congruent

Equation 7x - 12 = 3x + 28

7x - 3x = 28 + 12

4x = 40

x = 10

Angle Measurements = 58° & 58°

Problem 11 :

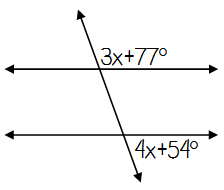
Type of angle pair ____

These angles are ____

Equation ____

x = ____

Angle Measurements = ____

Solution:

Type of angle pair Same-Side Exterior

These angles are Supplementary

Equation 3x + 77 + 4x + 54 = 180

7x + 131 = 180

7x = 49

x = 7

Angle Measurements = 98° & 82°

Problem 12 :

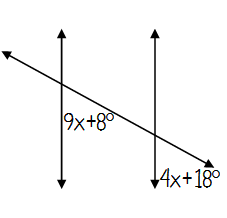
Type of angle pair ____

These angles are ____

Equation ____

x = ____

Angle Measurements = ___

Solution:

Type of angle pair Corresponding

These angles are Congruent

Equation 9x + 8 = 4x + 18

9x - 4x = 18 - 8

5x = 10

x = 2

Angle Measurements = 26° & 26°

Problem 13 :

Solve for n.

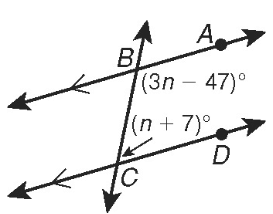
Solution :

Sum of same side interior angle = 180

3n - 47 + n + 7 = 180

3n + n - 47 + 7 = 180

4n - 40 = 180

4n = 180 + 40

4n = 220

n = 220/4

n = 44

Problem 14 :

Solve for x.

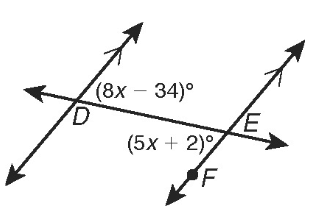
Solution :

Alternate interior angle will be equal.

8x - 34 = 5x + 2

8x - 5x = 2 + 34

3x = 36

x = 36/3

x = 12