FINDING SLOPE FROM TWO POINTS

Find the slope of the line through each pair of points.

Problem 1 :

(8, 10), (-7, 14)

Solution :

Given, (8, 10), (-7, 14)

Slope (m) = (y₂ – y₁)/(x₂ – x₁)

x₁ = 8, y₁ = 10, x₂ = -7, y₂ = 14

Slope (m) = (y₂ – y₁)/(x₂ – x₁)

= (14 – 10)/(-7 – 8)

= -4/15

Problem 2 :

(-3, 1), (-17, 2)

Solution :

Given, (-3, 1), (-17, 2)

Slope (m) = (y₂ – y₁)/(x₂ – x₁)

x₁ = -3, y₁ = 1, x₂ = -17, y₂ = 2

Substitute the values in Slope (m) = (y₂ – y₁)/(x₂ – x₁)

= (2 – 1)/(-17 – (-3))

= (2 – 1)/(-17 + 3)

= -1/14

Problem 3 :

(-20, -4), (-12, -10)

Solution :

Given, (-20, -4), (-12, -10)

Slope (m) = (y₂ – y₁)/(x₂ – x₁)

x₁ = -20, y₁ = -4, x₂ = -12, y₂ = -10

Substitute the values in Slope (m) = (y₂ – y₁)/(x₂ – x₁)

= (-10 - (-4))/(-12 – (-20))

= (-10 + 4)/(-12 + 20)

= -6/8

= -3/4

Problem 4 :

(-12, -5), (0, -8)

Solution :

Given, (-12, -5), (0, -8)

Slope (m) = (y₂ – y₁)/(x₂ – x₁)

x₁ = -12, y₁ = -5, x₂ = 0, y₂ = -8

Substitute the values in Slope (m) = (y₂ – y₁)/(x₂ – x₁)

= (-8 – (-5))/(0 - (-12))

= (-8 + 5)/(0 + 12)

= -3/12

= -1/4

Problem 5 :

(-19, -6) and (15, 16)

Solution :

(-19, -6) and (15, 16)

Slope (m) = (y₂ – y₁)/(x₂ – x₁)

x₁ = -19, y₁ = -6, x₂ = 15, y₂ = 16

Substitute the values in Slope (m) = (y₂ – y₁)/(x₂ – x₁)

 = (16 – (-6))/(15 – (-19))

= (16 + 6)/(15 + 19)

= 22/34

= 11/17

Problem 6 :

(-6, 9) and (7, -9)

Solution :

Given, (-6, 9), (7, -9)

Slope (m) = (y₂ – y₁)/(x₂ – x₁)

x₁ = -6, y₁ = 9, x₂ = 7, y₂ = -9

Substitute the values in Slope (m) = (y₂ – y₁)/(x₂ – x₁)

= = (-9 - 9)/(7 – (-6))

= (-9 - 9)/(7 + 6)

= -18/13

Problem 7 :

(-18, -20) and (-18, -15)

Solution :

Given, (-18, -20), (-18, -15)

Slope (m) = (y₂ – y₁)/(x₂ – x₁)

x₁ = -18, y₁ = -20, x₂ = 18, y₂ = -15

Substitute the values in Slope (m) = (y₂ – y₁)/(x₂ – x₁)

= (-15 – (-20))/(18 – (-18))

= (-15 + 20)/(18 + 18)

= 5/0

= Undefined

Problem 8 :

(12, -18) and (11, 12)

Solution :

Given, (12, -18), (11, 12)

Slope (m) = (y₂ – y₁)/(x₂ – x₁)

x₁ = 12, y₁ = -18, x₂ = 11, y₂ = 12

Substitute the values in Slope (m) = (y₂ – y₁)/(x₂ – x₁)

= (12 – (-18))/(11 - 12)

= (12 + 18)/(11 -12)

= -30/1

= -30

Problem 9 :

The line that passes through the points (3, -7) and (14, k) has the slope of 5/6. Determine the exact value of k.

Solution :

Slope of the line passes through the points,

(3, -7) and (14, k)

Slope = (k - (-7)) / (14 - 3)

5/6 = (k + 7) / 11

5(11) = 6(k + 7)

55 = 6k + 42

6k = 55 - 42

6k = 13

k = 13/6

Problem 10 :

The triangle on the right has horizontal side AC and vertical side BC. If the line segment AB has slope of 11/5, determine the area of the trianglle ABC to the nearest tenth of a square centimeter.

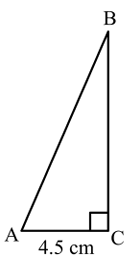
Solution :

Slope of the line segment AB = 11/5

The ratio between the vertical measure to the horizontal measure is the slope.

BC = 11x and AC = 5x

From the triangle shown above,

AC = 4.5

5x = 4.5

x = 4.5/5

x = 0.9 cm

Applying the value of x in 11x, we get 11(0.9) ==> 9.9 cm

Area of triangle ABC = (1/2) x 9.9 x 4.5

= 22.275 cm²

Problem 11 :

A line with slope 3/7 passes through the point (4, 2). Is the point (-130, -57) on this line? Explain.

Solution :

Slope = 3/7 ==> 0.428

To find the slope of the line, we can choose two points that lie on the line. The line passes through the points (4, 2) and (-130, -57)

Slope = (-57 -  2) / (-130 - 4)

= -59/(-134)

= 0.440

Since the slopes are not equal, the point (-130, -57) doesnot lie on the line which has the slope 3/7.

Problem 12 :

The rhombus shown in the diagram on the below has an area of 90 square units. Determine the slope of the line segment AD.

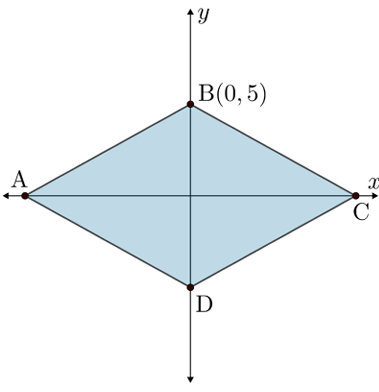
Solution :

Area of rhombus = 90

area of one triangle = 90/4

= 22.5 square units

1/2 x base x 5 = 22.5

2.5 x base = 22.5

base = 22.5/2.5

= 9

slope = rise / run

(-9, 0) and (0, -5)

= -5 - 0 / (0 + 9)

= -5/9