FINDING REMAINING ZEROS OF POLYNOMIAL FUNCTIONS WITH GIVEN ROOTS

Problem 1 :

If 1 is a zero of the polynomial

p(x) = ax² - 3(a - 1)x - 1

then find the value of 'a' and find other zero.?

Solution :

p(x) = ax² - 3(a - 1)x - 1

Since 1 is one of the zeros of the polynomial, we can put x = 1

p(1) = a(1)² - 3(a - 1)(1) - 1

0 = a - 3a + 3 - 1

0 = -2a + 2

2a = 2

a = 1

By applying the value of a in p(x), we get

p(x) = (1)x² - 3(1 - 1)x - 1

p(x) = x² - 1

Set p(x) = 0

x² - 1 = 0

(x + 1)(x - 1) = 0

x = -1 and x = 1

So, the another zero is -1.

Problem 2 :

What number should be added to the polynomial

x² - 5x + 4

so that 3 is the zero of the polynomial?

Solution :

Let p be the required value to be added.

p(x) = x² - 5x + 4 + p

Since x = 3, we can apply the value of x in p(x)

p(3) = 3² - 5(3) + 4 + p

0 = 9 - 15 + 4 + p

0 = 13 - 15 + p

0 = -2 + p

p = 2

So, 2 is the value to be added.

Problem 3 :

If one of the zeros of the cubic polynomial

x³ + ax² + bx + c is -1

then what will be the product of the other two zeros?

Solution :

Let p(x) = x³ + ax² + bx + c

When x = -1

p(-1) = (-1)³ + a(-1)² + b(-1) + c

p(-1) = -1 + a - b + c

0 = a - b + c - 1

a - b + c = 1

Problem 4 :

Obtain all other zeros of the polynomial

2x⁴ - 9x³+ 5x² + 3x - 1

if two of its zeros are 2 - √3 and 2 + √3?

Solution :

α = 2 - √3 and  β = 2 + √3

α + β = 2 - √3 + 2 + √3 ==>  4

α β = (2 - √3) (2 + √3) ==>  2² - √3²

= 4 - 3

= 1

Forming quadratic equation from the sum and product of roots,

x² - (α + β)x + α β = 0

x² - 4x + 1 = 0

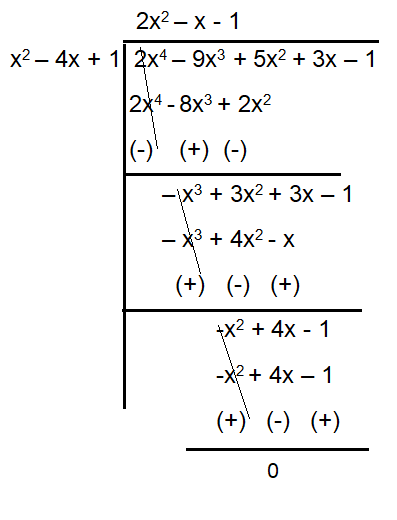
The quotient is 2x²-x-1, by factoring this quadratic polynomial, we get

2x²-x-1 = (2x + 1) (x - 1)

2x +1 = 0, then x = -1/2

x - 1 = 0, then x = 1

So, the remaining zeroes are -1/2 and 1.

Problem 5 :

Find the zeros of the polynomial

f(x) = x³ - 5x² -2x +24

if it is given that the product of its two zeros is 12?

Solution :

Let a, b and c be zeroes of the cubic polynomial.

Sum of zeroes = - coefficient of x²/coefficient of x³

a + b+ c = -(-5)/1

a + b + c = 5 -----(1) 

Product of zeroes = -constant/coefficient of x³

abc = -24/1

abc = -24

ab = 12 -----(2) (product of two of its zero)

c = -24/ab

c = -2

Applying the value of c in (1), we get

a + b - 2 = 5

a + b = 7

ab = 12

b = 12/a

Applying the value of b in a + b = 7

a + (12/a) = 7

a² + 12 = 7a

a² -7a + 12 = 0

(a - 3) (a - 4) = 0

a = 3 and a = 4

b = 4 and b = 3

So, the remaining zeroes are 3 and 4.

Problem 6 :

If the zeros of the polynomial f(x) = x³ – 3x² - 6x + 8 are of the form a-b, a, a+b, then find all the zeros.

Solution :

Sum of zeroes = - (-3)/1

a - b + a + a + b = 3 

3a = 3

a = 1

Product of zeroes = -8/1

a(a-b)(a+b) = -8

1(1 - b²) = -8

1 - b² = -8

b² = 9

b = 3, -3

If a = 1 and b = 3

a - b ==> 1 - 3 ==> -2

a = 1

a + b ==> 1 + 3 ==> 4

So, the zeroes are -2, 1 and 4.

Problem 7 :

If α, β are the two zeros of the polynomial

f(y) = y² - 8y + a and α² + β² = 40

find the value of ‘a’?

Solution :

f(y) = y² - 8y + a 

α² + β² = 40

(α + β)² - 2αβ = 40

Sum of zeroes (α + β) = -(-8)/1

(α + β) = 8 ----(1)

Product of zeroes (α β) = a/1

(α β) = a ----(2)

Applying the values of (1) and (2)

8² - 2a = 40

2a = 64 - 40

2a = 24

a = 12

So, the value of a is 12.