FINDING QUARTILES FROM STEM AND LEAF

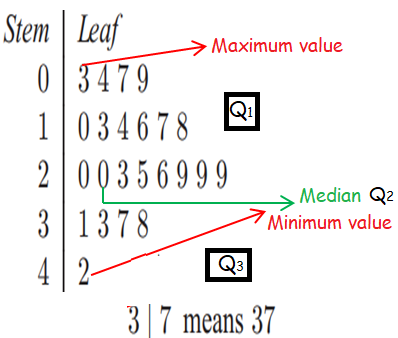
The difference between quartile 3 and quartile 1 is interquartile range.

To find interquartile range, we use the formula 

IQR = Q₃ - Q₁

Problem 1 :

For set of values, find

a) Minimum value           b) Maximum value

c)  the median      d)  the lower quartile

e)  the upper quartile    f)  the range

g)  the interquartile range

Solution :

a) Minimum value  = 20

b) Maximum value = 58

c)  the median

Total number of terms = 23

Middle value = (23 + 1)/2

= 12^th element

Median = 40

d)  the lower quartile

Quartile 1 is containing 11 elements.

middle value = (11 + 1)/2 ^th element

= 6^th element

Q₁ = 30

e)  the upper quartile

Quartile 3 is containing 11 elements.

middle value = (11 + 1)/2 ^th element

= 6^th element

Q₃ = 49

f)  the range :

Range = Largest value - smallest value

= 58 - 20

= 38

g)  the interquartile range 

= Q₃ - Q₁

= 49 - 30

= 19

Problem 2 :

The weight in kilograms of a particular brand of bags of fire wood is stated to be 20 kg, however some bags weight more than this and some weigh less. A sample of bags is carefully weighed and their weights are given in the ordered stem and leaf shown. 

a) Locate the median, upper and lower quartiles and maximum and minimum weights for the sample.

b) Find interquartile range and range.

Solution :

a)

Median :

Total number of elements = 24

Middle value (or) Median = 24/2 ^th element

= 12^th element

Median = 20.2

Lower quartile :

Quartile 1 is containing 11 elements.

middle value = (11 + 1)/2 ^th element

= 6^th element

Q₁ = 19.8

Upper quartile :

Quartile 3 is containing 11 elements.

middle value = (11 + 1)/2 ^th element

= 6^th element

Q₃ = 20.1

b) Interquartile range :

= 20.1 - 19.8

= 0.3

Range = Largest value - smallest value

= 22.3 - 18.8

= 3.5

Problem 3 :

For set of values, find

a) Minimum value           b) Maximum value

c)  the median      d)  the lower quartile

e)  the upper quartile    f)  the range

g)  the interquartile range

Solution :

a) Minimum value  = 3

b) Maximum value = 42

c)  the median

Total number of terms = 23

Middle value = (23 + 1)/2

= 12^th element

Median = 20

d)  the lower quartile

Quartile 1 is containing 11 elements.

middle value = (11 + 1)/2 ^th element

= 6^th element

Q₁ = 13

e)  the upper quartile

Quartile 3 is containing 11 elements.

middle value = (11 + 1)/2 ^th element

= 6^th element

Q₃ = 29

f)  the range :

Range = Largest value - smallest value

= 42 - 3

= 39

g)  the interquartile range 

= Q₃ - Q₁

= 29 - 13

= 16

Problem 4 :

The heights of 20 ten year olds are recorded in the following stem and leaf plot.

a) Find 

i) Median height

ii)  Upper and lower quartiles of the data.

Solution :

Total number of elements = 20

= 10^th element

= 124

Q₁ = 114

Q₃ = 131