FINDING QUADRATIC EQUATION FROM MAXIMUM AND MINIMUM WORKSHEET

Problem 1 :

Determine the equation of a quadratic function that has a minimum at (-2, -3) and passes through (-1, 1).

Solution

Problem 2 :

Determine the equation of a quadratic function that has a maximum at (2, 10) and passes through (1, 8).

Solution

Problem 3 :

Find the minimum of the parabola: y = 2x² + 8x + 9

(a) (-2, 1)     (b) (2, 33)     (c) (2, 17)

(d) (-2, -17)     (e) None of these

Solution

Problem 4 :

Find the maximum of the parabola: y = -3x² + 12x + 1

(a) (6, -5)     (b) (-2, -19)     (c) (2, 13)

(d) (1, 14)     (e) None of these

Solution

Problem 5 :

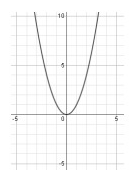
The graph of y = x² is shown in the standard (x, y) coordinate plane below. For which of the following equations is the graph of the parabola shifted 3 units to the right and 2 units down?

A) y = (x + 3)² - 2                 B) y = (x - 3)² - 2

C) y = (x + 3)² + 2                D) y = (x - 3)² + 2

Solution

Problem 6 :

The height of a bridge is given by the equation y = -3x² + 12x, where y is the height of the bridge (in miles) and x is the number of miles from the base of the bridge.

i. How far from the base of the bridge does the maximum height occur?

ii. What is the maximum height of the bridge?

A) i. 2 miles               ii. 12 miles

B) i. -2 miles              ii. 12 miles

C) i. 3 miles               ii. 9 miles

D) i. 3 miles              ii. 6 miles

Solution