FINDING PERIMETER OF RHOMBUS USING DIAGONALS

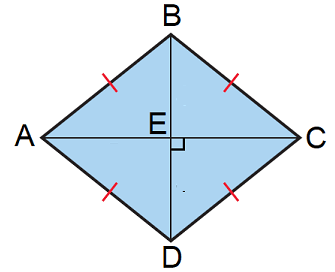
The diagonals of a rhombus will be perpendicular and they will bisect each other. 

Perimeter of rhombus = 4a

Here a is the side length of rhombus.

Problem 1 :

In the rhombus ABCD shown below, if the lengths of the diagonals AC and BD are 10 units and 8 units respectively, find its perimeter.

Solution :

AC = 10 units, then AE = EC = 5 units

BD = 8 units, then BE = ED = 4 units.

To find the perimeter, we find the side length of the rhombus.

Let us consider the triangle BEC.

BC² = BE² + EC²

BC² = 4² + 5²

BC² = 16 + 25

BC² = 41

BC = √41

Perimeter of rhombus = 4√41 units.

Problem 2 :

What is the perimeter of a rhombus whose diagonals are 16 cm and 30 cm?

Solution :

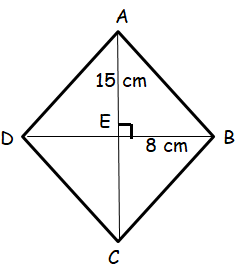
In triangle AEB,

AB² = AE² + EB²

AB² = 15² + 8²

AB² = 225 + 64

AB² = 289

AB = 17 cm

Perimeter of the rhombus ABCD = 4(17)

= 68 cm

Problem 3 :

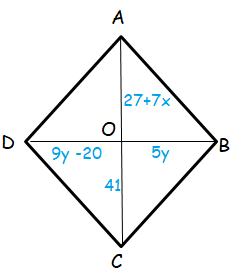
With in the information given below find x and y then find the perimeter of the rhombus.

Solution :

In rhombus, the diagonal will bisect each and 90 degree.

Applying the value of y in OB.

OB = 5(5) ==> 25

In triangle OCB,

BC² = OC² + OB²

BC² = 41² + 25²

BC² = 1681 + 625

BC² = 2306

BC = √2306

BC = 48.02

Perimeter of the rhombus = 4 (BC)

= 4(48.02)

= 192.08 units.

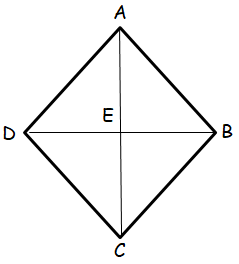
Problem 4 :

DB = 4x ft, EB = 30 ft

AC = (-y + 13) ft, AE = (5 - 2y) ft

Solve for x and y and find the perimeter.

Solution :

Applying the value of y in AC = (-y + 13)

AC = 14, AE = 7

AB² = AE² + EB²

AB² = 7² + 30²

AB² = 49 + 900

AB = √949

AB = 30.80

Perimeter = 4(30.80)

= 123.2