FINDING MISSING ANGLES OF PARALLELOGRAM

Consecutive Angles in Parallelogram

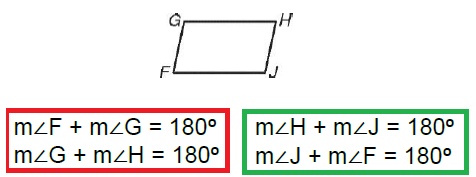
Opposite Angles in Parallelogram

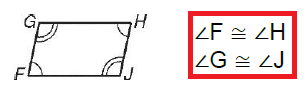
Problem 1 :

From the parallelogram given below, find the value of x, y and z.

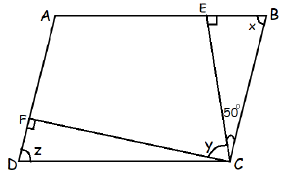
Solution :

In triangle EBC.

∠EBC + ∠BCE + ∠CEB = 180

x + 50 + 90 = 180

x + 140 = 180

x = 180 - 140

x = 40

Opposite angles are equal, x = z = 40

In triangle FDC.

∠FDC + ∠DCF + ∠CFD = 180

z + ∠DCF + 90 = 180

40 + 90 + ∠DCF = 180

130 + ∠DCF = 180

∠DCF = 180 - 130

∠DCF = 50

z + ∠DCF + y + 50 = 180

40 + 50 + y + 50 = 180

140 + y = 180

y = 180 - 140

y = 40

Problem 2 :

If one angle of a parallelogram is 24 degree less than twice the smallest angle then, find the largest angle of the parallelogram.

Solution :

Let the smallest angle be x

Larger angle measure = 2x - 24

Sum of consecutive angles = 180

x + 2x - 24 = 180

3x - 24 = 180

3x = 180 + 24

3x = 204

x = 204/3

x = 68

The largest angle measure = 2(68) - 24

= 136 - 24

= 112

So, the largest angle measure is 112.

Problem 3 :

In a parallelogram PQRS, if

∠P = (3x − 5)° and ∠Q = (2x + 15)°

then find the value of x.

Solution :

Since ∠P and ∠Q are consecutive integers, sum of the consecutive integers = 180.

∠P + ∠Q = (3x − 5) + (2x + 15)

3x + 2x - 5 + 15 = 180

5x + 10 = 180

5x = 170

x = 170/5

x = 34

Problem 4 :

If PQRS is a parallelogram, then ∠P − ∠R is

(a) 90° (b) 45° (c) 60° (d) 0°

Solution :

In any parallelogram, the opposite angles will be equal.

∠P  =  ∠R

∠P − ∠R = 0

Problem 5 :

Two adjacent angles of a parallelogram are 3x - 4 and 3x + 10. Find the angles of parallelogram.

Solution :

Adjacent angles are 3x - 4 and 3x + 10.

Sum of adjacent angles (Consecutive angles) = 180

3x - 4 + 3x + 10 = 180

6x + 6 = 180

6x = 180 - 6

6x = 174

x = 174/6

x = 29

So, the angles are 83 and 97.

Problem 6 :

One angle of a parallelogram is 60 degree. Find its opposite angle and the adjacent angle.

Solution :

Sum of adjacent angels = 180

One of the angle = 60

Adjacent angle = 180 - 60

= 120

In parallelogram, opposite angle will be equal. Opposite angle 60 degree is also 60 degree.