FINDING MEDIAN FOR UNGROUPED DATA

Find the median of the following data :

Problem 1 :

2, 5, 1, 5, 2, 1, 2, 3, 2, 3, 1

Solution :

Ascending order of the given data

1, 1, 1, 2, 2, 2, 2, 3, 3, 5, 5

Number of values given = 11 (odd)

Median = [(N + 1)/2]^th value

Median = 12/2 = 6^th value

Hence the median is 2.

Problem 2 :

8, 5, 1, 3, 7, 1, 1, 7, 1, 8, 7

Solution :

Ascending order of the given data

1, 1, 1, 1, 3, 5, 7, 7, 7, 8, 8

Number of values given = 11 (odd)

Median = [(N + 1)/2]^th value

Median = 12/2 = 6^th value

Hence the median is 5.

Problem 3 :

18, 22, 17, 20, 19, 20, 22, 19, 29, 18, 23, 25, 22, 24, 23, 22, 18, 20, 22, 20

Solution :

Ascending order of the given data 

17, 18, 18, 18, 19, 19, 20, 20, 20, 20, 22, 22, 22, 22, 22, 23, 23, 24, 25, 29

Number of given observations = 20

Median = [(N/2)^th observation + ((N/2) + 1)^th observation] / 2

Median = [(20/2)^th value + ((20/2) + 1)^th value] / 2

= (10^th value + 11^th value) / 2

= (20 + 22) / 2

= 42/2

= 21

Problem 4 :

42, 28, 32, 35, 24, 32, 48, 32, 32, 24, 35, 28, 30, 35, 45, 32, 28, 32, 42, 42, 30

Solution :

Ascending order of the given data

24, 24, 28, 28, 28, 30, 30, 32, 32, 32, 32, 32, 32, 35, 35, 35, 42, 42, 42, 45, 48

Number of values given = 21 (odd)

Median = [(N + 1)/2]^th value

Median = 22/2 = 11^th value

Hence the median is 32.

Problem 5 :

The number of children per house on one block:

1, 4, 2, 3, 3, 2, 6, 2, 4, 2, 0, 3, 0.

Solution :

Ascending order of the given data

0, 0, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 6

Number of values given = 13 (odd)

Median = [(N + 1)/2]^th value

Median = 14/2 = 7^th value

Hence the median is 2.

Problem 6 :

The number of movies watched each month last year: 2, 0, 3, 0, 0, 8, 6, 5, 0, 1, 2, 3

Solution :

Ascending order of the given data

0, 0, 0, 0, 1, 2, 2, 3, 3, 5, 6, 8

Number of given observations = 12

Median = [(N/2)^th observation + ((N/2) + 1)^th observation] / 2

Median = [(12/2)^th value + ((12/2) + 1)^th value] / 2

= (6^th value + 7^th value) / 2

= (2 + 2) / 2

= 4/2

= 2

Problem 7 :

The number of units being taken by students in one class: 12, 5, 11, 10, 10, 11, 5, 11, 11, 11, 10, 12.

Solution :

Ascending order of the given data

5, 5, 10, 10, 10, 11, 11, 11, 11, 11, 12, 12

Number of given observations = 12

Median = [(N/2)^th observation + ((N/2) + 1)^th observation] / 2

Median = [(12/2)^th value + ((12/2) + 1)^th value] / 2

= (6^th value + 7^th value) / 2

= (11 + 11) / 2

= 22/2

= 11

Problem 8 :

The number of hours of sleep per night for the past two weeks: 8, 5, 7, 8, 8, 6, 6, 6, 6, 9, 7, 8, 8, 8.

Solution :

Ascending order of the given data

5, 6, 6, 6, 6, 7, 7, 8, 8, 8, 8, 8, 8, 9

Number of given observations = 12

Median = [(N/2)^th observation + ((N/2) + 1)^th observation] / 2

Median = [(14/2)^th value + ((14/2) + 1)^th value] / 2

= (7^th value + 8^th value) / 2

= (7 + 8) / 2

= 15/2

= 7.5

Problem 9 :

A teacher asked his class of 20 students, “What is your age?” Their responses are shown on the line plot below

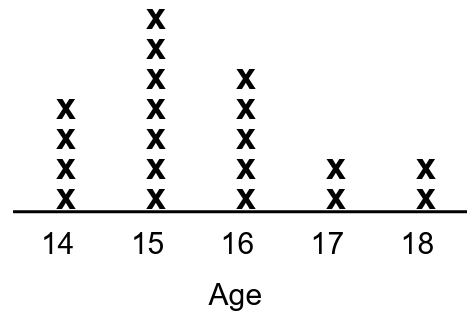
Find the mean, median, and mode of the data.

Solution :

Mean :

Mean = [14(4) + 15(7) + 16(5) + 17(2) + 18(2)] / (4 + 7 + 5 + 2 + 2)

= (56 + 105 + 80 + 34 + 36) / 20

= 311/20

= 15.55

Median :

Number of terms (N) = 20 (even)

= [N/2^th term + (N/2) + 1^th term]/2

= (10th term + 11th term)/2

= (15+15)/2

= 15

Mode :

Here 15 is repeating more number of times. Then mode is 15.

Problem 10 :

If x, 13, 15, 18, x + 1, x + 3, 30, 32, 35, 41 are ten observation in an ascending order with median 24, find the value of x.

Solution :

Median = 24

The given data is in ascending order.

x, 13, 15, 18, x + 1, x + 3, 30, 32, 35, 41

n = 10

Median = [N/2^th term + (N/2) + 1^th term]/2

= (5^th term + 6^th term)/2

(x + 1 + x + 3)/2 = 24

(2x + 4)/2 = 24

2x + 4 = 48

2x = 44

x = 44/2

x = 22

So, the value of x is 22.