FINDING MAXIMUM AND MINIMUM VALUES OF QUADRATIC EQUATION

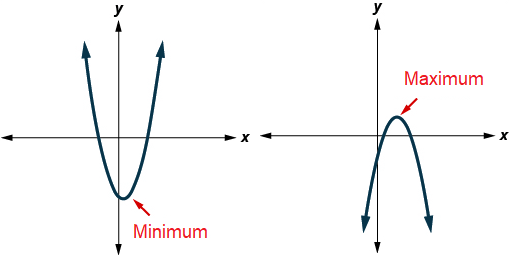
In general the graphical form of the quadratic function will the shape of u. It may be open upward or downward.

• Maximum point is the highest point of the parabolic path.
• Minimum point is the lowest point of the parabolic path.

To find maximum or minimum point of the quadratic equation we follow two ways.

(i) Converting into the vertex form

(ii) Using formula

Problem 1 :

Determine the equation of a quadratic function that has a minimum at (-2, -3) and passes through (-1, 1).

Solution:

The vertex form of the quadratic equation

y = a(x - h)² + k

Vertex (h, k) = (-2, -3)

y = a(x + 2)² - 3

It is passes through the point (x, y) = (-1, 1).

1 = a(-1 + 2)² - 3

1 = a(1)² - 3

1 = a - 3

a = 4

By applying a = 4 in above equation

y = 4(x + 2)² - 3

y = 4(x² + 4 + 4x) - 3

y = 4x² + 16 + 16x - 3

y = 4x² + 16x + 13

Problem 2 :

Determine the equation of a quadratic function that has a maximum at (2, 10) and passes through (1, 8).

Solution:

The vertex form of the quadratic equation

y = a(x - h)² + k

Vertex (h, k) = (2, 10)

y = a(x - 2)² + 10

It is passes through the point (x, y) = (1, 8).

8 = a(1 - 2)² + 10

8 = a(-1)2 + 10

8 = a + 10

a = -2

By applying a = -2 in above equation

y = -2(x - 2)² + 10

y = -2(x² - 4x + 4) + 10

y = -2x² + 8x - 8 + 10

y = -2x² + 8x + 2

Problem 3 :

Find the minimum of the parabola: y = 2x² + 8x + 9

(a) (-2, 1)     (b) (2, 33)     (c) (2, 17)

(d) (-2, -17)     (e) None of these

Solution:

y = 2x² + 8x + 9

Because the coefficient of x² is positive, the parabola is open upward.

Formula to find x-coordinate of the vertex is

x = -b/2a

Substitute a = 2 and b = 8.

x = -8/2(2)

x = -2

By applying x = -2 in equation,

y = 2(-2)² + 8(-2) + 9

= 8 - 16 + 9

y = 1

So, the minimum value is (-2, 1).

So, option (a) is correct.

Problem 4 :

Find the maximum of the parabola: y = -3x² + 12x + 1

(a) (6, -5)     (b) (-2, -19)     (c) (2, 13)

(d) (1, 14)     (e) None of these

Solution:

y = -3x² + 12x + 1

Because the coefficient of x² is negative, the parabola is open upward.

Formula to find x-coordinate of the vertex is

x = -b/2a

Substitute a = -3 and b = 12.

x = -12/2(-3)

= -12/-6

x = 2

By applying x = 2 in equation,

y = -3(2)² + 12(2) + 1

= -12 + 24 + 1

y = 13

So, the maximum value is (2, 13).

So, option (c) is correct.

Problem 5 :

The graph of y = x² is shown in the standard (x, y) coordinate plane below. For which of the following equations is the graph of the parabola shifted 3 units to the right and 2 units down?

A) y = (x + 3)² - 2                 B) y = (x - 3)² - 2

C) y = (x + 3)² + 2                D) y = (x - 3)² + 2

Solution:

y = x²

Shifted 3 units to the right.

y = (x - 3)²

Then shifted 2 units down.

y = (x - 3)² - 2

So, option (B) is correct.

Problem 6 :

The height of a bridge is given by the equation y = -3x² + 12x, where y is the height of the bridge (in miles) and x is the number of miles from the base of the bridge.

i. How far from the base of the bridge does the maximum height occur?

ii. What is the maximum height of the bridge?

A) i. 2 miles               ii. 12 miles

B) i. -2 miles              ii. 12 miles

C) i. 3 miles               ii. 9 miles

D) i. 3 miles              ii. 6 miles

Solution:

y = -3x² + 12x

i. 

To find x-coordinate of vertex

x = -b/2a

Substitute a = -3 and b = 12

x = -12/2(-3)

= 12/6

x = 2 miles

ii.

To find y-coordinate of vertex

y = -3x² + 12x

By applying x = 2 in above equation

y = -3(2)² + 12(2)

 = -12 + 24

y = 12 miles

So, option (A) is correct.