FINDING MAXIMUM AND MINIMUM OF QUADRATIC FUNCTION

The graphical form of a quadratic function will be a parabola (u shpae). In which the maximum and minimum value will be there at vertex.

To find the maximum or minimum value from the quadratic equation, we have the following ways.

(i) Converting into the vertex form

(ii) Using formula

Find the maximum or minimum value of the following function.

Problem 1 :

y = x² - 4x + 1

Solution :

Method 1 :

y = x² - 4x + 1

Write the coefficient of x as a multiple of 2.

y = [x² - 2 ⋅ x ⋅ 2 + 2² - 2² + 1]

y = [(x - 2)² - 2² + 1]

y = [(x - 2)² - 4 + 1]

y = (x - 2)² - 3

It is exactly in the form of 

y = a(x - h)² + k

Here a = 1 > 0, then the parabola opens up.

Vertex is at (2, -3).

So,

minimum is at x = 2 and the minimum value = -3.

Method 2 :

y = x² - 4x + 1

a = 1, b = -4 and c = 1

x = -b/2a

x = -(-4)/2(1)

x = 4/2

x = 2

By applying the value of x in the given equation, we get

y = 2² - 4(2) + 1

y = 4 - 8 + 1

y = 5 - 8

y = -3

So, the minimum point is at (2, -3).

Problem 2 :

y = -x² - x + 1

Solution :

y = -x² - x + 1

Factoring negative

y = -[x² + x - 1]

Here a = -1 < 0, then the parabola opens down.

Vertex is at (-1/2, 5/4).

So,

minimum is at x = -1/2 and the minimum value = 5/4.

Problem 3 :

y = 5x² - 3

Solution :

y = 5x² - 3

y = 5(x - 0) ² - 3

Here a = 5 > 0, the parabola opens up.

Vertex (h, k) ==> (0, -3)

The minimum is at x = 0 and minimum value = -3.

Minimum point is (0, -3).

Problem 4 :

y = (1/2)x² - x - 4

Solution :

y = (1/2)x² - x - 4

Here a = 1/2 > 0, the parabola opens up.

Vertex (h, k) ==> (1, -4.5)

The minimum is at x = 1 and minimum value = -4.5

Minimum point is  (1, -4.5).

Problem 5 :

The cables between the two towers of the Tacoma Narrows Bridge in Washington form a parabola that can be modeled by

y = 0.00016x² − 0.46x + 507

where x and y are measured in feet. What is the height of the cable above the water at its lowest point?

Solution :

a = 0.00016, b = -0.46 and c = 507

x = -(-0.46) / 2(0.00016)

= 0.46/0.00032

x = 1437.5

Approximately 1438 ft.

y = 0.00016(1438)² − 0.46(1438) + 507

= 330.85 - 661.48 + 507

= 176.37

Height of the cable above the water is about 176 ft.

Problem 6 :

The parabola shows the path of your first golf shot, where x is the horizontal distance (in yards) and y is the corresponding height (in yards). The path of your second shot can be modeled by the function f(x) = −0.02x(x − 80). Which shot travels farther before hitting the ground? Which travels higher?

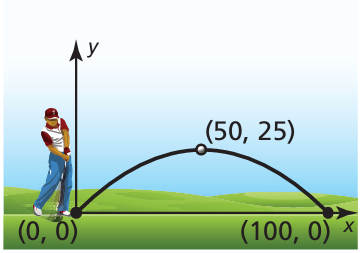
Solution :

Maximum height of the first shot :

By observing the graphm, the maximum height of the first shot is 25 yards.

Maximum height of the second shot :

f(x) = −0.02x(x − 80)

= -0.02x² + 1.6x

a = -0.02, b = 1.6 and c = 0

x = -1.6/2(-0.02)

= 1.6/0.04

= 40

When x = 40, f(40) = −0.02(40)(40 − 80)

f(40) = -0.8(-40)

= 32 yards

The maximum height reached by the second shot is 32 yards.

Discussing abobt x-intercepts :

In the first shot, it covers the horizontal distance of 100 yards.

In the second shot,

f(x) = −0.02(x - 0)(x − 80)

x = 0 and x = 80

it covers the horizontal distance of 80 yards.

• Because 100 yards > 80 yards, the first shot travels farther.
• Because 32 yards > 25 yards, the second shot travels higher.