FINDING LIMITS FROM A GRAPH PRACTICE FOR AP CALCULUS BC

Problem 1 :

The graph of the function f is shown. Which of the following statements about f is true ?

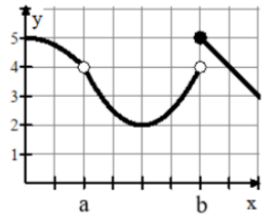
Option A :

lim _{x -> a} f(x) = 4

Approaching b from left side, we get 4

Approaching b from right side, we get 5. Which means

 lim _{x -> b} f(x) = undefined

lim _{x -> a} f(x) = 4 ≠ lim _{x -> b} f(x)

So, it is false.

Option B :

lim _{x -> a-} f(x) = 4 and lim _{x -> a+} f(x) = 4

So, lim _{x -> a} f(x) = 4. Then it is true.

Option C :

lim _{x -> b} f(x) = 4 and lim _{x -> b} f(x) = 5

Then it is false.

Option D :

It is false.

Option E :

lim _{x -> a}- f(x) = lim _{x -> a}+ f(x) = 4

The given says does not exists. So, it is false.

So, answer is option B.

Problem 2 :

The figure below shows the graph of a function f with domain 0 ≤ x < 6. Which of the following statements are true ?

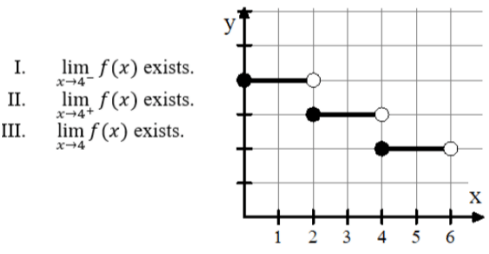
Solution :

lim _{x -> 4-} f(x) = 3

lim _{x -> 4+} f(x) = 2

lim _{x -> 4} f(x) = does not exists.

So, the answer is C.

Problem 3 :

The graph of the function f is shown below. For which of the following values of c does lim _{x -> c} f(x) = 2 ?

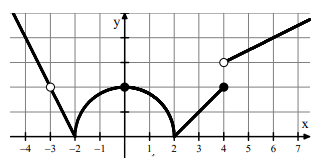
Solution :

lim _{x -> c} f(x) = 2

The output is 2, when x = -3 and 0.  So, option C is correct.

Problem 4 :

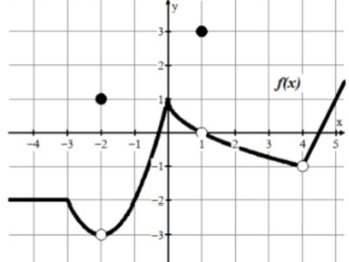
Evaluate each of the following from the above graph :

1)  f(-2) =

2) lim _x->-2 f(x) = 

3) f(1) = 

4)  f(4) = 

5) lim _x->-4 f(x) =

6) lim _x->0 f(x) =

Solution :

1)  f(-2) = 1

2) lim _x->-2 f(x) 

Tracing the function, we get -3. So, the value lim _x->-2 f(x) = -3.

3) f(1) = 3

4)  f(4)

At x = 4, we don't see the filled circle. The curve does not pass through any point, so it is undefined.

So, f(4) = undefined.

5) lim _x->-4 f(x) = -2

6) lim _x->0 f(x) = 1

Because the curve passes through the point (0, 1).

Problem 5 :

Let f be the function that is defined for all real numbers x. Of the following, which is the best representation of the statement lim _{x -> 4} f(x) = 8.

a) The value of the function f at x = 4 is 8.

b) The value of the function f at x = 8 is 4.

c) As x approaches 4, the values of f(x) approach 8.

d) As x approaches 8, the values of f(x) approach 4.

Solution :

c) As x approaches 4, the values of f(x) approach 8.

Problem 6 :

The function f satisfies lim _x->3 f(x) = 6. Which of the following could be the graph of f ?

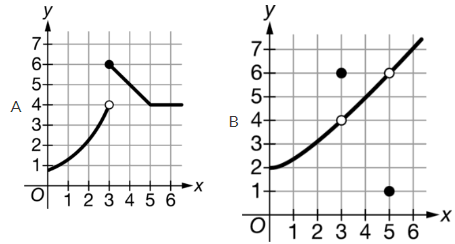
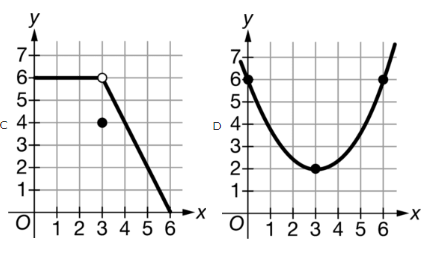
Solution :

Option A :

lim _x->3- f(x) = 4 and lim _x->3+ f(x) = 6. So, lim _x->3 f(x) = does not exists. Option A is incorrect.

Option C :

lim _x->3- f(x) = 6 and lim _x->3+ f(x) = 6. So, lim _x->3 f(x) = 6.

f(3) = 4.

So, option C is correct.

Problem 7 :

In order for the line y = a to be a horizontal asymptote of h(x), which of the following must be true?

A) lim_x→a+ h(x) = ∞          B) lim_x→a− h(x) = −∞

C) lim_x→∞ h(x) = ∞            D) lim _x→−∞ h(x) = a

E) lim _x→−∞ h(x) = ∞

Solution :

The output is a. Since there is a horizontal asymptote, x approaches +∞  and - ∞, the output is a. So, the answer is 

D) lim _x→−∞ h(x) = a