FINDING LENGTH OF ARC IN CIRCLE

The arc length s, of a circle of radius r with central angle θ given by

arc length (l) or s = rθ

l = (θ/360) x 2πr

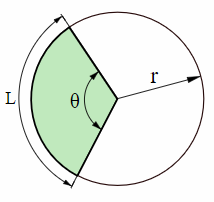
If s denotes the length of the arc of a circle of radius r subtended by a central angle θ, find the missing quantity.

Problem 1 :

s = 6.24 meters, θ = 2.6 radians, r =?

Solution :

s = θ × r

6.24 = 2.6 × r

r = 6.24 / 2.6

r = 2.4 m

Problem 2 :

r = 2/3 feet, s = 14 feet, θ =?

Solution :

s = θ × r

14 = θ × 2/3

θ = (14 × 3) / 2

r = 21 radians

Find the length s. Round the answer to three decimal places.

Problem 3 :

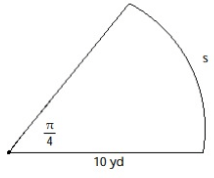
Solution :

Given, radius r = 10 yd

Central angle θ = π/4 = 45˚

arc length = 2πr (θ/360)

= 2 × 3.14 (10) (45˚/360˚)

= 7.854 yd

So, arc length is 7.854 yd.     

Problem 4 :

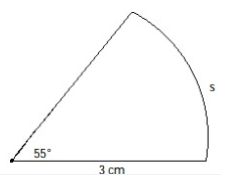
Solution :

Given, radius r = 3 cm

Central angle θ = 55˚

arc length = 2πr (θ/360)

= 2 × 3.14 (3) (55˚/360˚)

= 2.88 cm

So, arc length is 2.88 cm.       

Problem 5 :

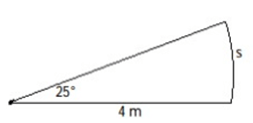
Solution :

Given, radius r = 4 m

Central angle θ = 25˚

Arc length = (θ/360) ⋅ 2πr

= 2 × 3.14 (4) (25˚/360˚)

= 1.745 m

So, arc length is 1.745 m.      

Problem 6 :

For a circle of radius 4 feet, find the arc length s subtended by central angle 60˚. Round to the nearest hundredth.

Solution :

Given, radius r = 4 feet

Central angle θ = 60˚

Arc length = (θ/360) ⋅ 2πr

= 2 × 3.14 (4) (60˚/360˚)

= 4.19 ft

So, arc length is 4.19 ft.            

Problem 7 :

A pendulum swings though an angle of 30˚ each second. If the pendulum is 35 inches long. How far does its tip move each second? If necessary, round the answer to two decimal places.

Solution :

Given, central angle θ = 30˚

Radius r = 35 inches

Arc length = (θ/360) ⋅ 2πr

= (30/360) ⋅ 2π(35)

= (1/12) ⋅ 2(22/7)(35)

= 18.3 inches