FINDING LENGTH OF A LINE SEGMENT

Problem 1 :

What is the approximate length of RS with endpoints R(2, 3) and S(4, -1)?

Solution :

Given, R(2, 3) and S(4, -1)

x₁ = 2,  y₁ = 3, x₂ = 4,  y₂ = -1

RS = √[(x₂ – x₁)² + (y₂ – y₁)²]  

= √[(4 – 2)² + ((-1) – 3)²]

= √[(2)² + (-4)²]

= √[4 + 16]

= √20

= 4.5

So, the approximate length is 4.5 units.

Problem 2 :

What is the approximate length of AB with endpoints A(-3, 2) and B(1, -4)?

Solution :

Given, A(-3, 2) and B(1, -4)

x₁ = -3,  y₁ = 2, x₂ = 1,  y₂ = -4

RS = √[(x₂ – x₁)² + (y₂ – y₁)²] 

= √[(1 – (-3))² + (-4 – 2)²]

= √[(4)² + (-6)²]

= √[16 + 36]

= √52

= 7.2

So, the approximate length is 7.2 units.

Problem 3 :

The endpoints of MN are M(-3, -9) and N(4, 8). What is the approximate length of MN?

Solution :

Given, M(-3, -9) and N(4, 8)

x₁ = -3,  y₁ = -9, x₂ = 4,  y₂ = 8

MN = √[(x₂ – x₁)² + (y₂ – y₁)²] 

= √[(4 – (-3))² + (8 – (-9)²]

= √[(7)² + (17)²]

= √[49 + 289]

= √338

= 18.4

So, the approximate length is 18.4 units.

Find the length of the segment. Round to the nearest tenth of a unit.

Problem 4 :

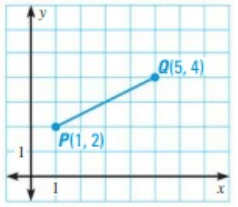
Solution :

Given, P(1, 2) and Q(5, 4)

x₁ = 1,  y₁ = 2, x₂ = 5,  y₂ = 4

PQ = √[(x₂ – x₁)² + (y₂ – y₁)²] 

= √[(5 – 1)² + (4 – 2)²]

= √[(4)² + (2)²]

= √[16 + 4]

= √20

= 4.5

So, the approximate length is 4.5 units.

Problem 5 :

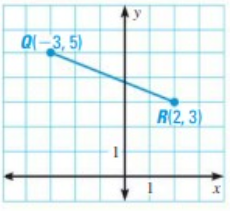
Solution :

Given, Q(-3, 5) and Q(2, 3)

x₁ = -3,  y₁ = 5, x₂ = 2,  y₂ = 3

PQ = √[(x₂ – x₁)² + (y₂ – y₁)²] 

= √[(2 – (-3))² + (3 – 5)²]

= √[(5)² + (-2)²]

= √[25 + 4]

= √29

= 5.385

So, the approximate length is 5.385 units.

Problem 6 :

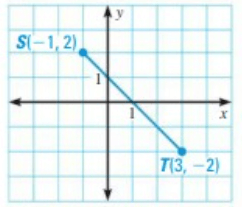
Solution :

Given, S(-1, 2) and T(3, -2)

x₁ = -1,  y₁ = 2, x₂ = 3,  y₂ = -2

PQ = √[(x₂ – x₁)² + (y₂ – y₁)²] 

= √[(3 – (-1))² + ((-2) – 2)²]

= √[(4)² + (-4)²]

= √[16 + 16]

= √32

= 5.7

So, the approximate length is 5.7 units.