FINDING LCM AND HCF USING VENN DIAGRAM

To find LCM and HCF of two numbers using venn diagram, we have to follow the steps given below.

Step 1 :

Write the prime factors of the given numbers.

Step 2 :

 Draw two circles to represent the factors of given numbers.

Step 3 :

The common factors should be placed in the intersection part and other numerical values should be fixed in the respective circles based on the number that we have in the question.

Step 4 :

Finding the product of prime factors that we find in the intersection part, we will get the greatest common divisor.

By multiplying all the values that we find inside the circles, we will get the least common multiple.

Find the highest common factor (HCF) of each pair of numbers.

Problem 1 :

21 and 49

Solution:

21 = 3 × 7

49 = 7 × 7

hcf-and-lcm-venn-diagram-q1.png

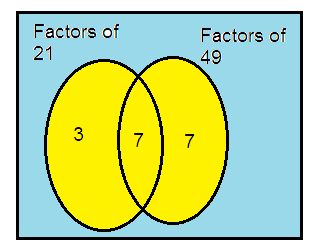
So, the HCF of 21 and 49 is 7.

Problem 2 :

35 and 45

Solution:

35 = 5 × 7

45 = 5 × 9

hcf-and-lcm-venn-diagram-q2.png

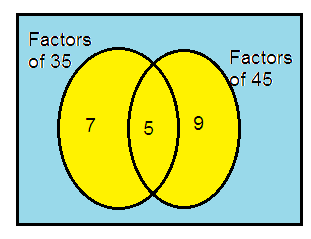
So, the HCF of 35 and 45 is 5.

Problem 3 :

18 and 24

Solution:

18 = 2 × 3 × 3

24 = 2 × 2 × 2 × 3

hcf-and-lcm-venn-diagram-q3.png

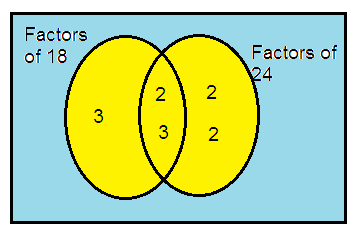
So, the HCF of 18 and 24 is

= 2 × 3

= 6

Problem 4 :

18 and 45

Solution:

18 = 2 × 3 × 3

45 = 5 ×  3 × 3

hcf-and-lcm-venn-diagram-q4.png

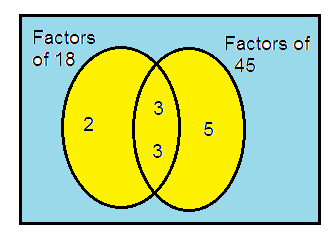
So, the HCF of 18 and 45 is

= 3 × 3

= 9

Problem 5 :

30 and 75 

Solution:

30 = 2 × 3 × 5

75 = 3 × 5 × 5

hcf-and-lcm-venn-diagram-q5.png

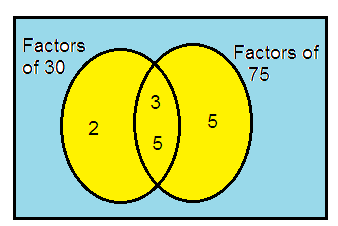
So, the HCF of 30 and 75 is

= 3 × 5

= 15

Problem 6 :

28 and 42

Solution:

28 = 2 × 2 × 7

42 = 2 × 3 × 7

hcf-and-lcm-venn-diagram-q6.png

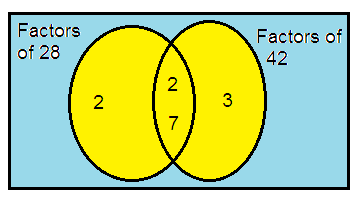
So, the HCF of 28 and 42 is

= 2 × 7

= 14

Problem 7 :

60 and 90

Solution:

60 = 2 × 2 × 3 × 5

90 = 2 × 3 × 3 × 5

hcf-and-lcm-venn-diagram-q7.png

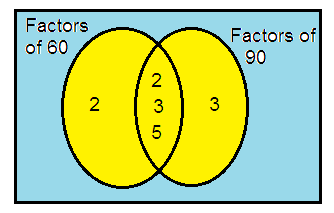
So, the HCF of 60 and 90 is

= 2 × 3 × 5

= 30

Problem 8 :

48 and 64

Solution:

48 = 2 × 2 × 2 × 2 × 3

64 = 2 × 2 × 2 × 2 × 2 × 2

hcf-and-lcm-venn-diagram-q8.png

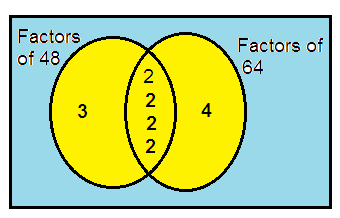
So, the HCF of 48 and 64 is

= 2 × 2 × 2 × 2

= 16

Find the lowest common multiple (LCM) of each pair of numbers.

Problem 9 :

15 and 35

Solution:

15 = 3 × 5

35 = 7 × 5

hcf-and-lcm-venn-diagram-q9.png

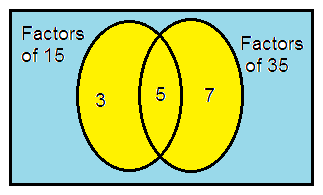
So, the LCM of 15 and 35 is

= 3 × 5 × 7

= 105

Problem 10 :

14 and 22

Solution:

14 = 2 × 7

22 = 2 × 11

hcf-and-lcm-venn-diagram-q10.png

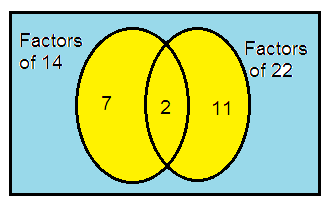
So, the LCM of 14 and 22 is

= 2 × 7 × 11

= 154

Problem 11 :

15 and 21

Solution:

15 = 3 × 5

21 = 3 × 7

hcf-and-lcm-venn-diagram-q11.png

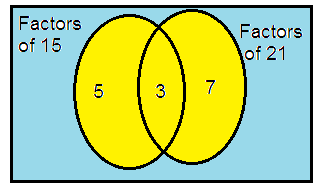
So, the LCM of 15 and 21 is

= 3 × 5 × 7

= 105

Problem 12 :

9 and 33

Solution:

9 = 3 × 3 

33 = 3 × 11 

hcf-and-lcm-venn-diagram-q12.png

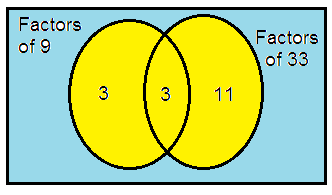
So, the LCM of 9 and 33 is

= 3 × 3 × 11

= 99

Problem 13 :

12 and 15

Solution:

12 = 2 × 2 × 3

15 = 3 × 5

hcf-and-lcm-venn-diagram-q13.png

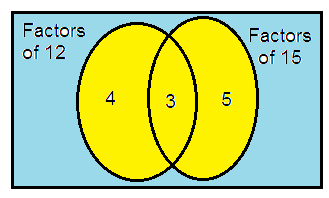
So, the LCM of 12 and 15 is

= 4 × 3 × 5

= 60

Problem 14 :

18 and 30

Solution:

18 = 2 × 3 × 3

30 = 2 × 3 × 5

hcf-and-lcm-venn-diagram-q14.png

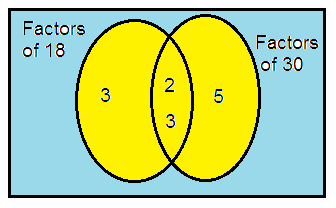
So, the LCM of 18 and 30 is

= 2 × 3 × 3 × 5

= 90

Problem 15 :

16 and 20

Solution:

16 = 2 × 2 × 2 × 2

20 = 2 × 2 × 5

hcf-and-lcm-venn-diagram-q15.png

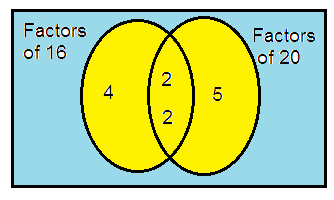
So, the LCM of 16 and 20 is

= 2 × 2 × 4 × 5

= 80

Problem 16 :

24 and 30

Solution:

24 = 2 × 2 × 2 × 3

30 =  2 × 3 × 5

hcf-and-lcm-venn-diagram-q16.png

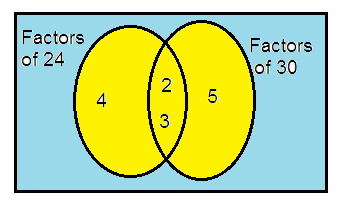
So, the LCM of 24 and 30 is

= 2 × 3 × 4 × 5

= 120

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More