FINDING INVERSE OF LOGARITHMIC FUNCTION

To find inverse of a linear function, we follow the steps given below.

Step 1 :

The given equation will be in the form y =, Derive the equation for x = 

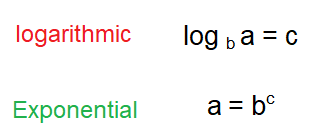
Step 2 :

After solving for x, change x as f^-1(x) and y as x.

Relationship between f(x) and and f^-1(x) :

Domain of the function f(x) = Range of f^-1(x)

Range of the function f(x) = Domain of f^-1(x)

Problem 1 :

y = log₃ (4^x - 4)

Solution:

y = log₃ (4^x - 4)

Interchange x and y.

x = log₃ (4^y - 4)

3^x = 4^y - 4

Add 4 from both sides,

3^x + 4 = 4^y

y = log₄ (3^x + 4)

Problem 2 :

y = log₂ (3x³)

Solution:   

y = log₂ (3x³)

Interchange x and y.

x = log₂ (3y³)

2^x = 3y³

Problem 3 :

y = log₂ (x + 5) - 9

Solution:

y = log₂ (x + 5) - 9

Interchange x and y.

x = log₂ (y + 5) - 9

2^x = (y + 5) - 9

Add 9 from both sides,

2^{x + 9} = y + 5

y = 2^{x + 9} - 5

Problem 4 :

y = log₅ (3x³ - 6)

Solution:

y = log₅ (3x³ - 6)

Interchange x and y.

x = log₅ (3y³ - 6)

5^x = 3y³ - 6

Add 6 from both sides,

5^x + 6 = 3y³

Problem 5 :

y = -7 log₆ (-3x)

Solution:

y = -7 log₆ (-3x)

Interchange x and y.

x = -7 log₆ (-3y)

Problem 6 :

y = log₆ (4x + 4)

Solution:

y = log₆ (4x + 4)

Interchange x and y.

x = log₆ (4y + 4)

6^x = 4y + 4

Subtract 4 from both sides,

6^x - 4 = 4y

Problem 7 :

y = 6 log₂ (2^x - 7)

Solution:

y = 6 log₂ (2^x - 7)

Interchange x and y.

x = 6 log₂ (2^y - 7)

Add 7 from both sides,

Problem 8 :

y = 6 log₅ (-4x) - 7

Solution:

y = 6 log₅ (-4x) - 7

Interchange x and y.

x = 6 log₅ (-4y) - 7