FINDING INVERSE FROM THE GIVEN ORDERED PAIRS

Find the inverse for each relation.

Problem 1 :

{(1, -3), (-2, 3), (5, 1), (6, 4)}

Solution:

Let R = {(1, -3), (-2, 3), (5, 1), (6, 4)}

R^-1 = {(-3, 1), (3, -2), (1, 5), (4, 6)}

Problem 2 :

{(-5, 7), (-6, -8), (1, -2), (10, 3)}

Solution:

Let R = {(-5, 7), (-6, -8), (1, -2), (10, 3)}

R^-1 = {(7, -5), (-8, -6), (-2, 1), (3, 10)}

In each problem, find the inverse of the function then graph both the function and its inverse.

Problem 3 :

f(x) = (2, 4) (-5, 3) (-2, -3) (1, 1) (-4, -4) (-1, -2) (3, -1)

f^-1(x) = 

Solution:

f(x) = (2, 4) (-5, 3) (-2, -3) (1, 1) (-4, -4) (-1, -2) (3, -1)

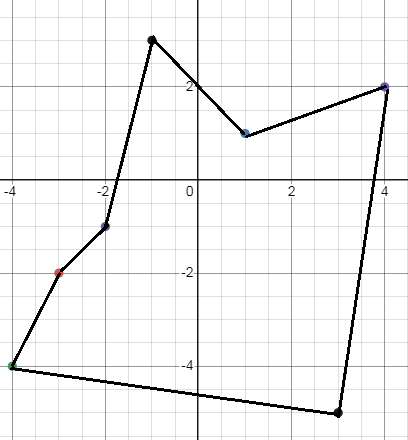
f^-1(x) = (4, 2) (3, -5) (-3, -2) (1, 1) (-4, -4) (-2, -1) (-1, 3)

f(x) :

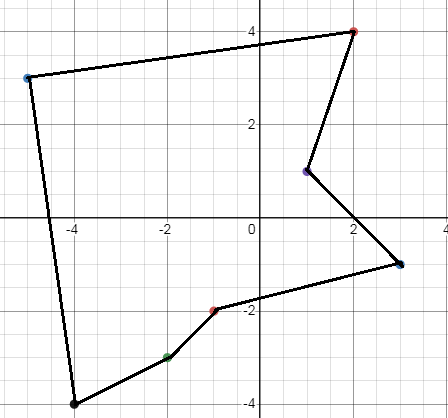
f^-1(x) :

Problem 4 :

h(x) = (0, 0) (-2, 4) (-1, -4) (2, 2) (-3, -3) (-4, 4) (1, -1) 

h^-1(x) = 

Solution:

h(x) = (0, 0) (-2, 4) (-1, -4) (2, 2) (-3, -3) (-4, 4) (1, -1) 

h^-1(x) = (0, 0) (4, -2) (-4, -1) (2, 2) (-3, -3) (4, -4) (-1, 1)

h(x) :

h^-1(x) :

Does the function have an inverse function?

Problem 5 :

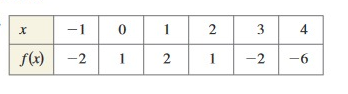
Solution:

The inputs -1 and 3 are associated with -2.

From the arrow diagram, it is clear

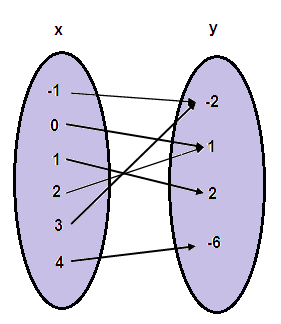
different inputs are giving the same output. So, it is not one to one.

Problem 6 :

Solution:

Each input is having different output.

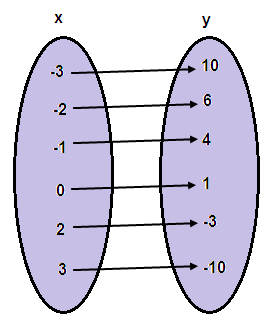
So, it is one to one.

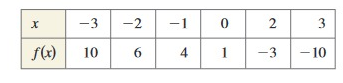
Use the table of values for y = f(x) to complete a table for y = f^-1(x).

Problem 7 :

Solution:

f^-1(x) :

Problem 8 :

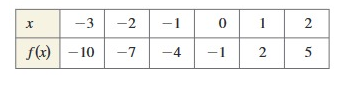
Solution:

f^-1(x) :

Problem 9 :

The function given by f(x) = k(x³ + 3x - 4) has an inverse function, and f^-1(-5) = 2. Find k.

Solution:

Given, f(x) = k(x³ + 3x - 4)

Since the inverse of f(x) exists and f^-1(-5) = 2, 

then f(2) = -5

Put x = 2 in the function  f(x) = k(x³ + 3x - 4)

f(2) = k(2³ + 3(2) - 4)

-5 = k(8 + 6 - 4)

-5 = 10k

k = -1/2

Problem 10 :

Think About It The function given by f(x) = k(2 - x - x³) has an inverse function, and f^-1(3) = -2. Find k.

Solution:

Given, f(x) = k(2 - x - x³)

Since the inverse of f(x) exists and f^-1(3) = -2, 

then f(-2) = 3

Put x = -2 in the function  f(x) = k(2 - x - x³)

f(-2) = k(2 - (-2) - (-2)³)

3 = k(2 + 2 + 8)

3 = 12k

k = 1/4

Problem 11 :

Your wage is $8.00 per hour plus $0.75 for each unit produced per hour. So, your hourly wage in terms of the number of units produced is

(a) Find the inverse function.

(b) What does each variable represent in the inverse function?

(c) Determine the number of units produced when your hourly wage is $22.25.

Solution :

x be the number of units he works

Required wages y = 8 + 0.75x

a) The required function is 

y = 8 + 0.75x

Inverse function.

Exchange x and y

x = 8 + 0.75y

Solve for y, 

x - 8 = 0.75y

y = (x - 8)/0.75

f^-1(x) = (x - 8)/0.75

In the original function x represents hours and y represent wages.

b)  In the inverse function x represents wages and f^-1(x) represents number of hours.

(c)  f^-1(x) = (22.25 - 8)/0.75

f^-1(x) = (22.25 - 8)/0.75

= 14.25/0.75

f^-1(x) = 19 units

Problem 12 :

You need a total of 50 pounds of two types of ground beef costing $1.25 and $1.60 per pound, respectively. A model for the total cost of the two types of beef is where is the number of pounds of the less expensive ground beef.

y = 1.25x + 1.60(50 - x)

(a) Find the inverse function of the cost function. What does each variable represent in the inverse function?

(b) Use the context of the problem to determine the domain of the inverse function.

(c) Determine the number of pounds of the less expensive ground beef purchased when the total cost is $73.

Solution :

a)  y = 1.25x + 1.60(50 - x)

y = 1.25x + 80 - 1.60x

y = -0.35x + 80

y = 80 -0.35x

x be the number of pounds of beef and y be the total cost.

Inverse function :

x = 80 - 0.35y

Solving for y,

0.35y = 80 - x

y = (80 - x)/0.35

f^-1(x) = (80 - x)/0.35

b) Here x be the total cost and f^-1(x) number of pounds of beef.

c) Total cost = 73

73 = 80 -0.35x

0.35x = 80 - 73

0.35x = 7

x = 7/0.35

x = 20

When number of pounds of beef is 20, the cost will be $73.