FINDING HORIZONTAL ASYMPTOTES OF EXPONENTIAL FUNCTIONS

Identify the asymptote and transformation from the parent function

f(x) = 4^x

i)  identify 3 points

ii) the asymptote

iii)  transformations from the parent function

f(x) = 4^x

iv) sketch

Problem 1 :

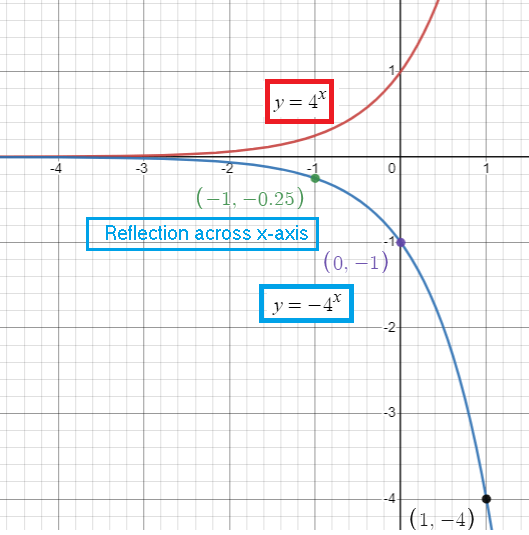
f(x) = -4^x

Solution:

i) Identifying 3 points :

Three points are (-1, -1/4) (0, -1) and (1, -4).

ii) Horizontal asymptote:

Considering the function f(x) = a(b^x) + c

Horizontal asymptote y = c

So, the horizontal asymptote is at y = 0.

iii) Transformations:

Since y = -y, then it is reflection across x-axis.

iv) Sketching :

Problem 2 :

f(x) = 4^x + 2

Solution:

i) Identifying 3 points :

Three points are (-1, 9/4) (0, 3) and (1, 6).

ii) Horizontal asymptote:

Considering the function f(x) = 4^x + 2

So, the horizontal asymptote is at y = 2.

iii) Transformations:

Shift 2 units up

iv) Sketching :

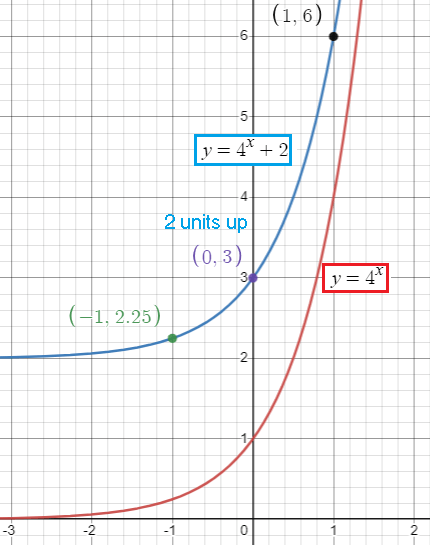
Problem 3 :

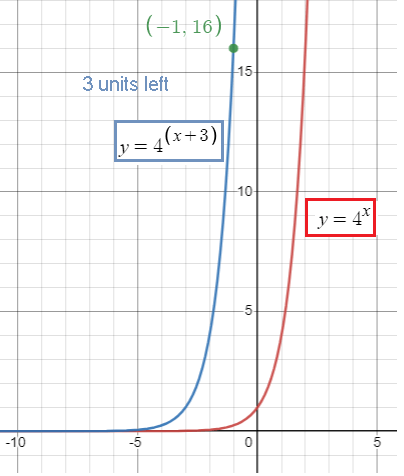
f(x) = 4^x+3

Solution:

i) Finding 3 points :

Three points are (-1, 16) (0, 64) and (1, 256).

ii) Horizontal asymptote:

horizontal asymptote is at y = 0.

iii)  Transformations:

Shift 3 units left

iv) Sketching the graph :

Problem 4 :

f(x) = (1/4)^x

Solution:

i) Finding 3 points :

Three points are (-1, 4) (0, 1) and (1, 1/4).

ii)  Horizontal asymptote:

 f(x) = (1/4)^x 

So, the horizontal asymptote is at y = 0.

iii)  Transformations:

There is no transformation.

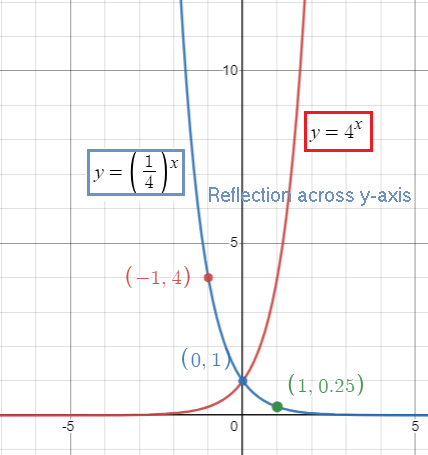
Problem 5 :

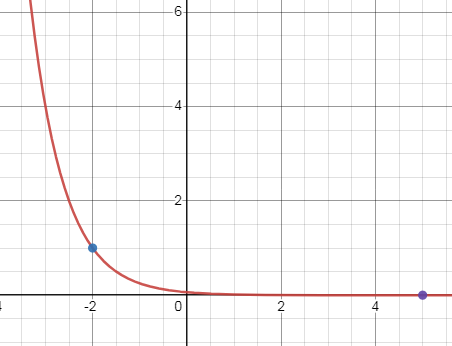
f(x) = 4^-x-2

Find the following :

Solution:

Parent :

f(x) = 4^x

Transformation:

Reflection across y-axis and shifting 2 units left

Domain:

All real number

Range:

(0, ∞), {y| y > 0}

Asymptote:

Horizontal asymptote y = 0

Problem 6 :

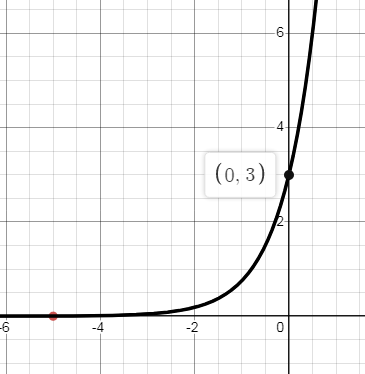
f(x) = (3)(4)^x

Solution:

Parent :

f(x) = 4^x

Transformation:

Vertical stretch with the factor of 3 units.

Domain:

All real number

Range:

(0, ∞), {y| y > 0}

Asymptote:

Horizontal asymptote y = 0