FINDING FUNCTION VALUES FROM A GRAPH OF PERIODIC FUNCTION

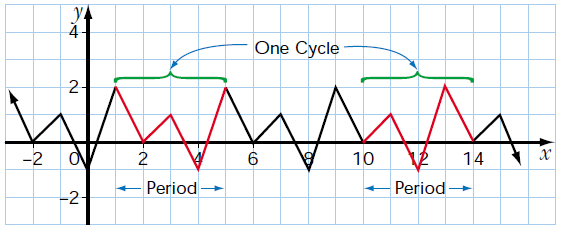
Problem 1 :

The graph has the period of 7. Find the value of 

a) f(6)     b)  f(20)

Solution :

Since the graph is periodic with the period of 7, for every 7 units repeatedly we will get the same y-values.

a) f(6) = -1

b) f(13) = 

then f(6 + 7) = f(13) = -1

f(13 + 7) = f(20) = -1

To reach 20 in the horizontal axis, we have to complete two cycles and in the third cycle, we will get the same y-value.

Interval of the first cycle is 1 to 7

Interval of the second cycle is 7 to 14

Interval of the third cycle is 14 to 21

From end of the third cycle, we have to move back 1 unit. Instead of doing this, we can move back the same one unit from the end of the first cycle. Then -1 is the value of f(20).

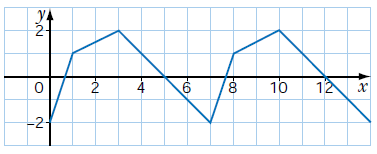
Problem 2 :

The function shown is periodic

a) Find the period of the function

b) Find f(4), f(5), f(8) and f(13)

c) Find the amplitude of the function.

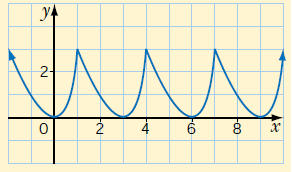
Solution :

The given function is periodic. By finding the horizontal length we can find the period.

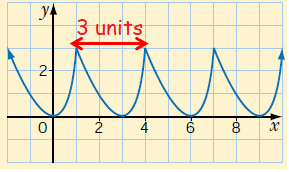
a) Period of the function is 3 units. For every 3 units of horizontal distance the y-values will be the same. Interval of period of x-values is 1 to 4.

b) From the graph shown, f(4) = 3

i)  f(5) = f(2 + 3)

To reach f(5), from the end of the first cycle, we have to move 1 unit horizontally. Repeating the same thing in the cycle itself. That is, from the starting position of cycle f(1), we move forward 1 unit horizontally. We get 1 as the value of y.

Then, f(5) = 1

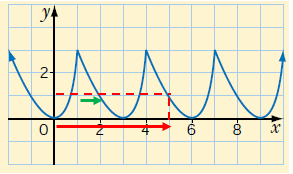
ii)  f(8) = f(5 + 3)

= f(5) (Here 3 is the period of the function)

The value of f(5) is 1. By observing the graph also the value of f(8) is 1.

iii)  f(13)

Question :

How many cycles can be completed with 13 but the cycle starts with 1 and with the period of 3 units.

Answer :

4 cycles can be completed with the period of 3.

First cycle : 1 to 4

second cycle : 4 to 7

Third cycle : 7 to 10

Fourth cycle : 10 to 13

So, y-value of end of the first cycle will the value of f(13). By observing the graph, f(4) = 3 then f(13) = 3.

c) Amplitude = (max - min)/2

= (3 - 0)/2

Amplitude = 1.5

Problem 3 :

A periodic function f has a period of 12. If f(7) = -2 and f(11) = 9, determine the value of 

i) f(43)     ii) f(79)     iii) f(95)     iv) f(-1)

Solution :

If f(7) = -2 and f(11) = 9

i) f(43)

To get 43, we decompose 43 as much as multiple of 12.

= f(7 + 3(12))

12 is the length of period, then f(43) and f(7) will be the same. So, the value of f(43) is -2

ii) f(79)

To get 79, we decompose 79 as much as multiple of 12.

= f(7 + 6(12))

= f(7)

f(79) = -2

iii) f(95) = f(11 + 7(12))

= f(11)

It is given that value of f(11) is 9. Then f(95) = 11

iv)  f(-1)

From x = 7, going back 12 units we will stand at -5. Distance between -5 to -1 is 4 units. From x = -5, we have to go back 4 units. Instead of doing this, we can do the same in the pattern. But we donot know the interval of the period and starting point. So, we try in another way.

Using the property, f(x + p) = f(x) where p is the period.

f(-1) = f(-1 + 12)

= f(11)

= 9

Problem 4 :

For a periodic function f(x) with period p, f(x + p) = f(x), and f(x + np) = f(x), where n is any integer. Consider the periodic function shown. 

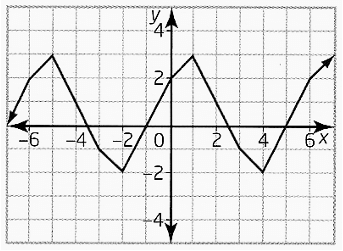
(a) What is the period of the function?

(b) Determine f(2) and f(5)

c) Predict f(8) and f(-10)

d) What is the amplitude of the function ?

e) Determine four x-values such that f(x) = 2.

Solution :

a)  While observing the graph, we see the pattern. The horizontal length of one pattern is 

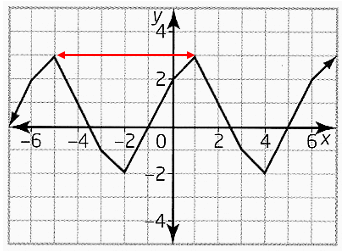
Distance from -5 to 1,

|-5| = 5 and |1| = 1

5 + 1 = 6 units

The length of period is 6 units.

b)  f(2) and f(5)

By observing the graph f(2) = 1 and f(5) = 0.

c) f(8)

Using the property, f(8) = f(2 + 6)

6 is the period

= f(2)

= 1

f(-10) 

The length of the period is 6 units. Going back,

interval of the first cycle is -5 to -11 

Here -10 lies in the the interval and the distance between -11 to -10 is 1 unit, so we have to move right from -11. Instead of doing this, we can do the same thing with the pattern from the shown graph above. The value of  f(-4) is 1. Then f(-10) is also 1.

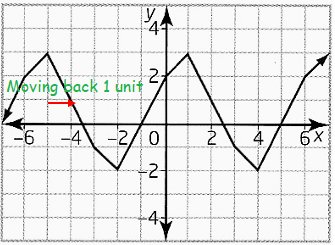
d) The height of the graph is 3. So, amplitude of the graph is 3.

e)  Drawing the horizontal line for y = 2, we get

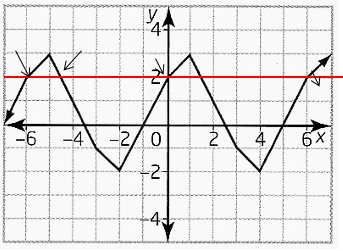
-6, -12, 0 and 6.