FINDING EXACT TRIG VALUES USING SPECIAL ANGLES

Find the exact value of each trigonometric function

Problem 1 :

Evaluate sin 225°

Solution :

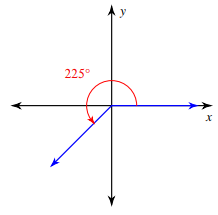
The given angle lies in the 3^rd quadrant. Using ASTC, the angle which lies in the 3rd quadrant if it is tan and its reciprocal cotangent, we should use positive sign. For other trigonometric ratios we should use negative sign.

θ = 225

Reference angle = θ - 180

= 225 - 180

= 45

sin 225° = -sin 45°

= -√2/2

Problem 2 :

Evaluate cos 150°

Solution :

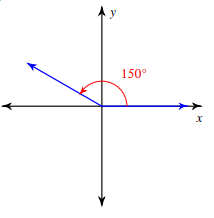
θ = 150

Since the angle lies in 2^nd quadrant, using ASTC we use negative sign.

Reference angle = 180 - θ

= 180 - 150

= 30

cos 150° = -cos 30°

= -√3/2

Problem 3 :

Evaluate tan 240°

Solution :

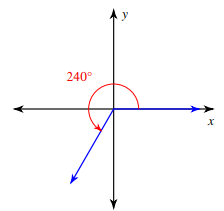
θ = 240

Since the angle lies in 3^rd quadrant, using ASTC we use positive sign.

Reference angle = θ - 180

= 240 - 180

= 60

tan 240° = tan 60°

= √3

Problem 4 :

Evaluate cos 135°

Solution :

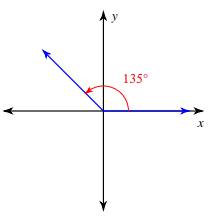
θ = 135

Since the angle lies in 2^nd quadrant, using ASTC we use negative sign.

Reference angle = 180 - θ

= 180 - 135

= 45

cos 135° = -cos 45°

= -√2/2

Problem 5 :

Evaluate tan 150°

Solution :

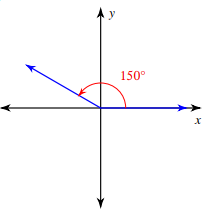
θ = 150

Since the angle lies in 2^nd quadrant, using ASTC we use negative sign.

Reference angle = 180 - θ

= 180 - 150

= 30

tan 150° = -tan 30°

= -1/√3

Problem 6 :

Evaluate cos 270°

Solution :

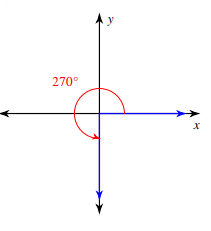
θ = 270

Since the angle lies in 3^rd quadrant, using ASTC we use negative sign.

Reference angle = θ - 180

= 270 - 180

= 90

cos 270° = -cos 90°

= 0

Problem 7 :

Evaluate cos 990°

Solution :

Since the given angle measure is more than 360, we divide the given angle by 360 and use the remainder.

cos 990 = cos (720 + 270)

cos 990 = cos 270

Since the angle lies in 3^rd quadrant, using ASTC we use negative sign.

Reference angle = θ - 180

= 270 - 180

= 90

cos 270° = -cos 90°

= 0

Problem 8 :

Evaluate

Solution :