FINDING EQUATION OF PARABOLA WITH X AND Y INTERCEPTS

To find equation of parabola with x and y-intercepts, we can use the following method.

y = a(x - p)(x - q)

Here p and q are x-intercepts and a is constant which is not equal to 0.

To find the value of a, we can apply the y-intercept. The sign of a will decide that the parabola opens up or opens down.

• If a > 0, the parabola opens up.
• If a < 0, the parabola opens down.

Equation of axis of symmetry :

The axis of symmetry lies halfway between the x-intercepts.

If p and q are x-intercepts, then equation of axis of symmetry is x = (p + q)/2

There are three possible situations for p and q.

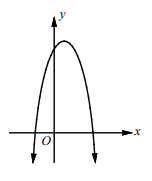	If p and q are different, the parabola will intersect x-axis at two different points.
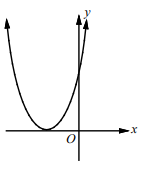	If p and q are same, the parabola will intersect x-axis at once.
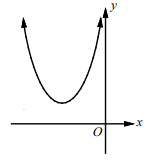	If p and q are not real, the parabola will not meet x-axis.

Problem 1 :

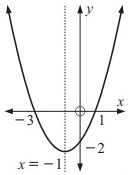
Sketch the parabola which has x-intercepts -3 and 1, and y-intercept -2.

i) Find equation of parabola

ii) Find the equation of the axis of symmetry.

Solution:

x- Intercepts: 

(-3, 0) (1, 0)

y- Intercept:

(0, -2)

Equation of parabola,

y = a (x - p) (x - q)

y = a (x + 3) (x - 1)

Substitute x = 0 and y = -2,

-2 = a (0 + 3) (0 - 1)

-2 = -3a

a = 2/3

y = 2/3 (x + 3) (x - 1)

The axis of symmetry lies halfway between the x-intercepts.

axis of symmetry = (-3 + 1)/2

= -2/2

= -1

So, axis of symmetry x = -1.

For each of the following:

i. Sketch the parabola

ii. Find the equation of the axis of symmetry.

Problem 2 :

x- intercepts 3 and -1, y- intercept -4

Solution:

x- Intercepts: 

(3, 0) (-1, 0)

y- Intercept:

(0, -4)

Equation of parabola,

y = a (x - p) (x - q)

y = a (x - 3) (x + 1)

Substitute x = 0 and y = -4,

-4 = a (0 - 3) (0 + 1)

-4 = -3a

a = 4/3

y = 4/3 (x - 3) (x + 1)

The axis of symmetry lies halfway between the x-intercepts.

axis of symmetry = (3 - 1)/2 

= 2/2

= 1

So, axis of symmetry x = 1.

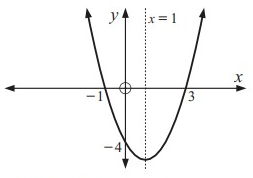
Problem 3 :

x- intercepts 2 and -2, y- intercept 4

Solution:

x- Intercepts: 

(2, 0) (-2, 0)

y- Intercept:

(0, 4)

Equation of parabola,

y = a (x - p) (x - q)

y = a (x - 2) (x + 2)

Substitute x = 0 and y = 4,

4 = a (0 - 2) (0 + 2)

4 = -4a

a = -1

y = -1 (x - 2) (x + 2)

The axis of symmetry lies halfway between the x-intercepts.

axis of symmetry = (-2 + 2)/2

= 0/2

= 0

So, axis of symmetry x = 0.

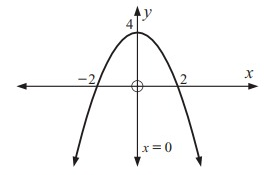
Problem 4 :

x- intercept -3 (touching), y- intercept 6

Solution:

x- Intercepts: 

At -3, the parabola touches x-axis twice.(-3, 0) (-3, 0)

y- Intercept:

(0, 6)

Equation of parabola,

y = a (x - p) (x - q)

y = a (x + 3) (x + 3)

Substitute x = 0 and y = 6,

6 = a (0 + 3) (0 + 3)

6 = 9a

a = 2/3

y = 2/3 (x + 3) (x + 3)

The axis of symmetry lies halfway between the x-intercepts.

axis of symmetry = (-3 - 3)/2

= -6/2

= -3

So, axis of symmetry x = -3.

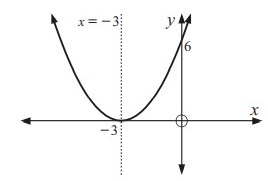
Problem 5 :

x- intercept 1 (touching), y- intercept -4

Solution:

x- Intercepts: 

At 1, the parabola touches x-axis twice. (1, 0) (1, 0)

y- Intercept:

(0, -4)

Equation of parabola,

y = a (x - p) (x - q)

y = a (x - 1) (x - 1)

Substitute x = 0 and y = -4,

-4 = a (0 - 1) (0 - 1)

-4 = a(1)

a = -4

y = -4 (x - 1) (x - 1)

The axis of symmetry lies halfway between the x-intercepts.

axis of symmetry = (1 + 1)/2

= 2/2

= 1

So, axis of symmetry x = 1.

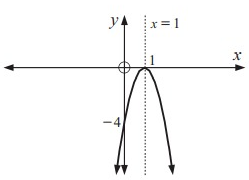
For each of the following find the equation of the axis of symmetry:

Problem 6 :

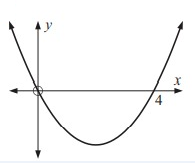
Solution:

The axis of symmetry lies halfway between the x-intercepts.

axis of symmetry = (0 + 4)/2

= 4/2

= 2

So, axis of symmetry x = 2.

Problem 7 :

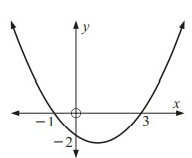
Solution:

The axis of symmetry lies halfway between the x-intercepts.

axis of symmetry = (-1 + 3)/2

= 2/2

= 1

So, axis of symmetry x = 1.

Problem 8 :

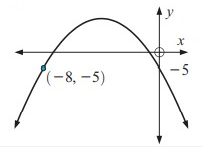
Solution:

By observing the figure, the x-intercepts are -7 and -1.

Equation of axis of symmetry = (-7 + (-1))/2

x = -8/2

x = -4

So, axis of symmetry x = -4.