FINDING EQUATION OF PARABOLA WITH VERTEX AND AXIS OF SYMMETRY

Problem 1 :

Write the equation the parabola  with vertex (-7, 4), axis of symmetry x = -7 and measure of latus rectum 6. a < 0

Solution :

Equation of axis of symmetry x = -7

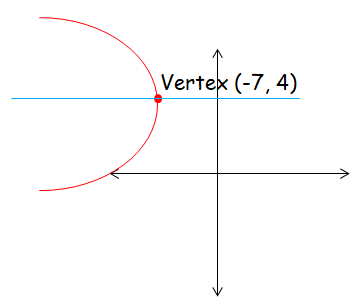
Here the equation is in the form x = -a, the parabola will be symmetric about x-axis.

Length of latus rectum = 6

4a = 6

a = 6/4

a = 3/2

Equation of parabola which is symmetric about x-axis and open leftward will be 

(y - k)² = -4a(x - h)

(y - 4)² = -4(3/2)(x - (-7))

(y - 4)² = -2(3)(x + 7)

(y - 4)² = -6(x + 7)

To get equation of parabola in general form, we expand the above

y² - 2y(4) + 4² = -6x - 42

y² - 8y + 16 = -6x - 42

y² - 8y  + 6x + 16 + 42 = 0

y² - 8y  + 6x + 58 = 0

Problem 2 :

Write the equation the parabola  with vertex (4, 3), axis of symmetry y = 3 and measure of latus rectum 4. a > 0

Solution :

Equation of axis of symmetry y = 3

Here the value of a is greater than 0. Let us make a graph with the given information.

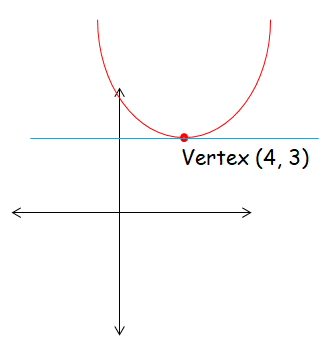
Here the equation is in the form y = a, the parabola will be symmetric about y-axis.

Length of latus rectum = 4

4a = 4

a = 4/4

a = 1

Equation of parabola which is symmetric about y-axis and open up will be 

(x - h)² = 4a(y - k)

(x - 4)² = 4(1)(y - 3)

x² -  2x(4) + 4² = 4y - 12

x² -  8x + 16 - 4y + 12 = 0

x² -  8x - 4y + 28 = 0

Problem 3 :

In the parabola shown in the graph, the point (2, -2) is called the _____ and the point (2, 0) is called the ____.

a)  The line  y = -4 is called the _________

b) The line x = 2 is called the _________

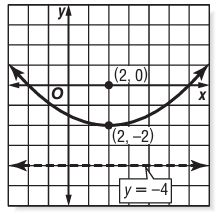
Solution :

From the given graph, it is clear that the vertex of the parabola is at (2, -2)

The point (2, 0) lies inside the parabola and it is at opposite of vertex, then this is focus of the parabola.

Finding the distance between vertex and focus is 4 units. Since it is open upward, equation of directrix will be in the form y = -a.

x = 2 is the vertical line that will divide the parabola into two equal parts. So, it is axis of symmetry. 

In the parabola shown in the graph, the point (2, -2) is called the Vertex and the point (2, 0) is called the Focus

a)  The line  y = -4 is called the directrix

b) The line x = 2 is called the axis of symmetry

Problem 4 :

Write the equation the parabola  with vertex (1, 3), axis of symmetry x = 1 and measure of latus rectum 2. a < 0

Solution :

Equation of axis of symmetry x = 1

Here the value of a is lesser than 0. The parabola is symmetric about x-axis and open leftward.

Length of latus rectum = 2

4a = 2

a = 2/4

a = 1/2

(y - k)² = -4a(x - h)

(y - 3)² = -4(1/2)(x - 1)

(y - 3)² = -2(x - 1)

y²  - 6y + 9 = -2x + 2

y²  - 6y + 9 + 2x - 2 = 0

y²  - 6y + 2x + 7 = 0