FINDING EQUATION OF PARABOLA WITH FOCUS AND DIRECTRIX

Problem 1 :

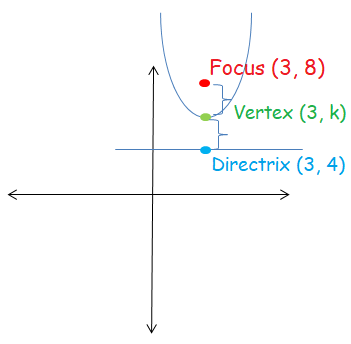
Write the equation of parabola which has focus at (3, 8) and directrix at y = 4.

Solution :

Equation of directrix y = 4

Focus is at (3, 8)

From this information, it is clear that the parabola is symmetric about y-axis.

Focus will be at opposite of vertex and it will lie inside the parabola. 3 is the x-coordinate of the vertex and k be the y-coordinate of vertex.

Distance between vertex and focus = distance between focus and directrix

(or)

Vertex point will be the midpoint of focus and directrix and the points are collinear.

Midpoint = (x₁ + x₂)/2, (y₁ + y₂)/2

= (3 + 3)/2, (8 + 4)/2

= 6/2, 12/2

= (3, 6)

So, the vertex is at (3, 6)

(x - h)² = 4a(y - k)

(x - 3)² = 4a(y - 6) ----(1)

Distance between vertex and focus :

√(x₂ - x₁)² + (y₂ - y₁)²

(3, 8) and (3, 6)

=√(3 - 3)² + (8 - 6)²

=√(3 - 3)² + (2)²

a = 2

By applying the value of a in (1), we get

(x - 3)² = 4(2)(y - 6)

(x - 3)² = 8(y - 6)

So, the required equation of parabola is (x - 3)² = 8(y - 6).

Problem 2 :

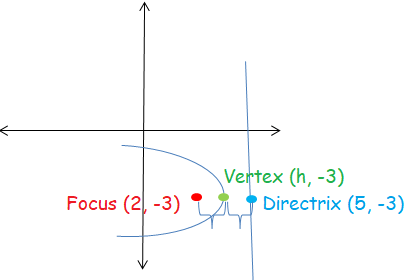
Write the equation of parabola which has focus at (2, -3) and directrix at x = 5

Solution :

Equation of directrix x = 5

Focus is at (2, -3)

From this information, it is clear that the parabola is symmetric about x-axis.

Vertex is at (h, -3), the point which is opposite of vertex and it lie on the directrix will be (5, -3)

Finding the midpoint of focus and directrix, we get vertex

(2, -3) and (5, -3)

= (2 + 5) / 2, (-3 - 3) / 2

= 7/2, -6/2

= (3.5, -3)

So, the vertex is at (3.5, -3)

(y - k)² = -4a(x - h)

(y - (-3))² = -4a(y - 3.5)

(y + 3)² = -4a(y - 3.5)----(1)

Finding the distance between vertex and focus, we get

(3.5, -3) and  (2, -3)

√(x₂ - x₁)² + (y₂ - y₁)²

= √(2 - 3.5)² + (-3 + 3)²

= √(-1.5)² 

a = 1.5

By applying the value of a in (1), we get

(y + 3)² = -4(1.5)(y - 3.5)

(y + 3)² = -6 (y - 3.5)

So, the required equation of parabola is 

(y + 3)² = -6 (y - 3.5)

Problem 3 :

Write the equation of parabola which has focus at (-4, -2) and directrix at x = -8

Solution :

Equation of directrix x = -8

Focus is at (-4, -2)

From this information, it is clear that the parabola is symmetric about x-axis.

Vertex is at (h, -2), the point which is opposite of vertex and it lie on the directrix will be (-8, -2)

Midpoint of focus and directrix = vertex

= (-4 -8)/2, (-2 - 2)/2

= -12/2, -4/2

= (-6, -2)

So, the parabola is opening to the right with the vertex (-6, -2). By applying this value in the standard form of parabola, we get

(y - k)² = 4a(x - h)

(y - (-2))² = 4a(x - (-6))

(y + 2)² = 4a(x + 6)  -----(1)

By finding the distance between vertex and focus, we will get the value of a.

(-6, -2) and  (-4, -2)

√(x₂ - x₁)² + (y₂ - y₁)²

= √(-6 + 4)² + (-2 + 2)²

= √(-2)² + 0

a = 2

By applying the value of a in (1), we get

(y + 2)² = 4(2) (x + 6) 

(y + 2)² = 8 (x + 6) 

So, the required equation is (y + 2)² = 8 (x + 6) .