FINDING EQUATION OF PARABOLA GIVEN FOCUS AND VERTEX

Problem 1 :

Find the equation of parabola with focus (5, 0) and vertex (5, 3).

Solution :

Always foucs and vertex will lie on the same line. The focus is below the vertex, the parabola opens down.

(x - h)² = -4a(y - k)

Here (h, k) is (5, 3)

(x - 5)² = -4a(y - 3) ----(1)

To find "a", let us find the distance between focus and vertex,

Distance between two points = √(x₂ - x₁)² + (y₂ - y₁)²

= √(5 - 5)² + (3 - 0)²

= √9

a = 3

By applying the value of a in (1), we get

(x - 5)² = -4(3)(y - 3)

(x - 5)² = -12(y - 3)

Problem 2 :

Find the equation of parabola whose focus is at (6, 3) and the vertex (2, 3) is given by.

Solution :

Always foucs and vertex will lie on the same line. The focus is at next to vertex. So the parabola opens right and it is symmetric about x-axis.

(y - k)² = 4a(x - h)

Here (h, k) is (2, 3)

(y - 3)² = 4a(x - 2) ----(1)

To find "a", let us find the distance between focus and vertex,

Distance between two points = √(x₂ - x₁)² + (y₂ - y₁)²

= √(6 - 2)² + (3 - 3)²

= √4² + 0²

a = 4

By applying the value of a in (1), we get

(y - 3)² = 4(4)(x - 2)

(y - 3)² = 16(x - 2)

Problem 3 :

Find the equation of parabola whose focus is at (-2, 4) and the vertex (1, 4) is given by.

Solution :

Always foucs and vertex will lie on the same line. The focus is in front of vertex. So the parabola opens left and it is symmetric about x-axis.

(y - k)² = -4a(x - h)

Here (h, k) is (1, 4)

(y - 4)² = -4a(x - 1) ----(1)

To find "a", let us find the distance between focus and vertex,

Distance between two points = √(x₂ - x₁)² + (y₂ - y₁)²

= √(1 - (-2))² + (4 - 4)²

= √3² + 0²

a = 3

By applying the value of a in (1), we get

(y - 4)² = -4(3)(x - 1)

(y - 4)² = -12(x - 1)

Problem 4 :

Write an equation of the parabola shown.

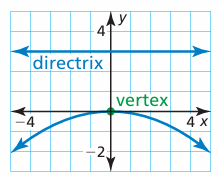
Solution :

The parabola opens down. The vertex of the parabola is at (0, 0).

Distasnce between vertex and focus = distance between vertex and directrix

(x - h)² = -4a(y - k)

(h, k) ==> (0, 0) and a = 3

(x - 0)² = -4(3)(y - 0)

x² = -12y

Problem 5 :

Write an equation of the parabola with vertex at (0, 0) and the given directrix or focus.

a)  directrix: x = −3

b)  focus: (−2, 0)

c)  focus: (0, 3/2)

Solution :

a) vertex is at (0, 0) and equation of directrix is x = -3

a = 3

From the given information, we know that the parabola opens down.

(y - k)² = -4a(x - h)

(y - 0)² = -4(3)(x - 0)

y² = -12x

b) Vertex is at (0, 0) and focus is at (-2, 0).

Distance between vertex and focus = 2

From the given information, the parabola is symmeteric about x-axis and open leftward.

(x - h)² = -4a(y - k)

(x - 0)² = -4(2)(y - 0)

x² = -8y

c) Vertex is at (0, 0) and focus is at (0, 3/2).

Distance between vertex and focus = 3/2

From the given information, the parabola is symmeteric about x-axis and open right side.

(x - h)² = 4a(y - k)

(x - 0)² = 4(3/2)(y - 0)

x² = 6y

Problem 6 :

Which of the following are possible coordinates of the point P in the graph shown? Explain.

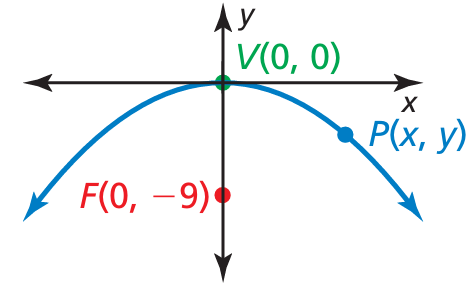
a)  (-6, -1)     b)  (3, -1/4)     c)  (4, -4/9)     d) (1, 1/36)      e)  (6, -1)    f)  (2, -1/18)

Solution :

The parabola is symmetric about y-axis and it opens downward parabola.

(x - h)² = -4a(y - k)

Distance between vertex and focus = a = 9

(x - 0)² = -4(9)(y - 0)

x² = -36y

So, the points a, b, c and e lies on the parabola.