FINDING EQUATION OF A PARALLEL LINE

Write down the equation of each of the following lines.

Example 1 :

Parallel to y = 3x + 5 and passing through (0, 2)

Solution :

y = 2x + 5 ----(1)

Comparing slope intercept form y = mx + c in (1), we get

Slope (m₁) = 2

Since the lines are parallel, slopes of two lines will be equal.

m₁ = m₂

Using Point Slope Form :

y - y₁ = m(x - x₁)

We have,

Slope (m) = 2, Point (x₁, y₁) = (0, 2)

y - 2 = 2(x - 0)

y - 2 = 2x

2x - y + 2 = 0

So, the equation of the line is 2x - y + 2 = 0.

Example 2 :

Parallel to y = 4x - 1 and passing through (0, 6)

Solution :

y = 4x - 1 ----(1)

Comparing slope intercept form y = mx + c in (1), we get

Slope (m₁) = 4

Since the lines are parallel, slopes of two lines will be equal.

m₁ = m₂

Using Point Slope Form :

y - y₁ = m(x - x₁)

We have,

Slope (m) = 4, Point (x₁, y₁) = (0, 6)

y - 6 = 4(x - 0)

y - 6 = 4x

4x - y + 6 = 0

So, the equation of the line is 4x - y + 6 = 0.

Example 3 :

Parallel to y = 5x and passing through (0, -3)

Solution :

y = 5x ----(1)

Comparing slope intercept form y = mx + c in (1), we get

Slope (m₁) = 5

Using Point Slope Form :

y - y₁ = m(x - x₁)

We have,

Slope (m) = 5, Point (x₁, y₁) = (0, -3)

y + 3 = 5(x - 0)

y + 3 = 5x

5x - y - 3 = 0

So, the equation of the line is 5x - y - 3 = 0.

Example 4 :

Parallel to y = -2x + 10 and passing through the origin

Solution :

y = -2x + 10 ----(1)

Comparing slope intercept form y = mx + c in (1), we get

Slope (m₁) = -2

Using Point Slope Form :

y - y₁ = m(x - x₁)

We have,

Slope (m) = -2, Origin (x₁, y₁) = (0, 0)

y - 0 = -2(x - 0)

y - 0 = -2x

2x + y - 0 = 0

So, the equation of the line is 2x + y - 0 = 0.

Example 5 :

Parallel to x + y = 8 and passing through (0, -4)

Solution :

x + y = 8

y = -x + 8 ----(1)

Comparing slope intercept form y = mx + c in (1), we get

Slope (m₁) = -1

Using Point Slope Form :

y - y₁ = m(x - x₁)

We have,

Slope (m) = -1, Origin (x₁, y₁) = (0, -4)

y + 4 = -1(x - 0)

y + 4 = -x

x + y + 4 = 0

So, the equation of the line is x + y + 4 = 0.

Example 6 :

Parallel to x - 2y + 3 = 0 and passing through (0, 5)

Solution :

x - 2y + 3 = 0

-2y = -x - 3

y = x/2 + 3/2 ----(1)

Comparing slope intercept form y = mx + c in (1), we get

Slope (m₁) = 1/2

Using Point Slope Form :

y - y₁ = m(x - x₁)

We have,

Slope (m) = 1/2, Origin (x₁, y₁) = (0, 5)

y - 5 = 1/2(x - 0)

y - 5 = x/2

2(y - 5) = x

2y - 10 = x

x - 2y + 10 = 0

So, the equation of the line is x - 2y + 10 = 0.

Example 7 :

Write down equation of the line parallel to line 1 and passes through A.

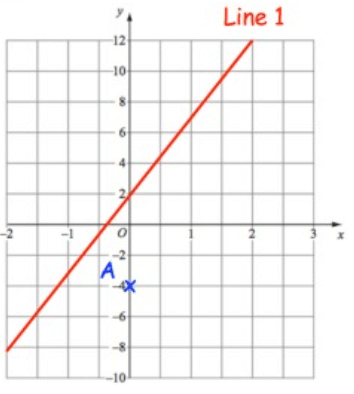
Solution :

Slope (m) = Rise/Run

= 10/2

m = 5

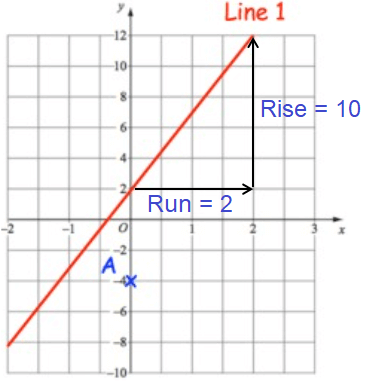
Drawing a line parallel to the given line using the slope 5.

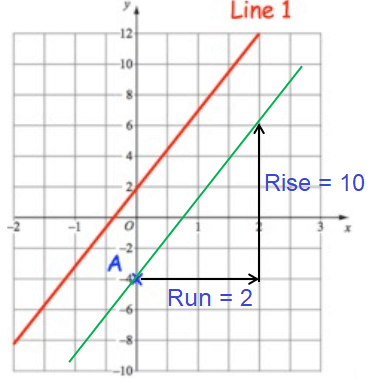
Equation of line passes through the point A will have the same slope 

y = 5x - 4

To check our equation, we select one of the point from the line that we have drawn. Say (2, 6)

Applying the point (2, 6) on the line :

6 = 5(2) - 4

6 = 10 - 4

6 = 6

Example 8 :

Write down equation of the line parallel to line 1 and passes through A.

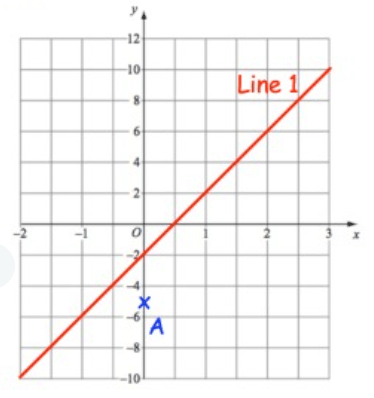
Solution :

To find the slope of the line, we the formula rise/run.

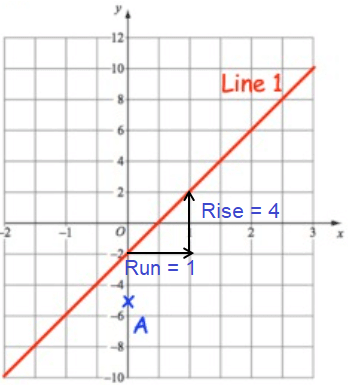
Slope (m) = Rise/Run

In graph, Rise = 4 and Run = 1

= 4/1

m = 4

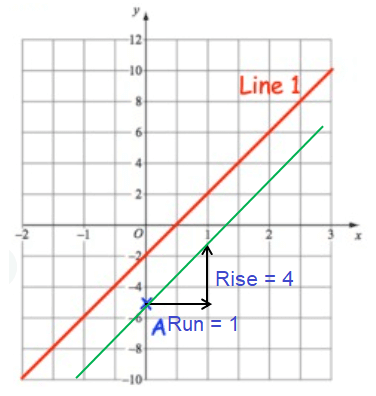
Equation of line passes through the point A will have the same slope 

y = 4x - 5

To check our equation, we select one of the point from the line that we have drawn. Say (2, 3)

Applying the point (2, 3) on the line :

3 = 4(2) - 5

3 = 8 - 5

3 = 3

Example 9 :

Write down equation of the line parallel to line 1 and passes through A.

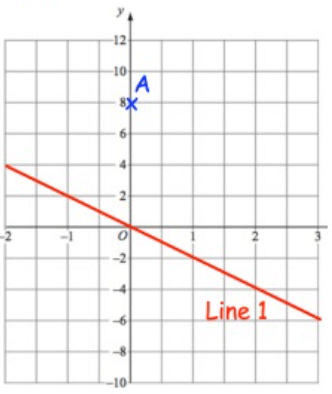
Solution :

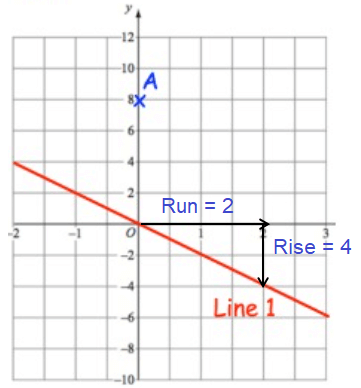
Slope (m) = Rise/Run

In graph, Rise = 2 and Run = 4, it is falling line. So it will have negative slope.

= -4/2

m = -2

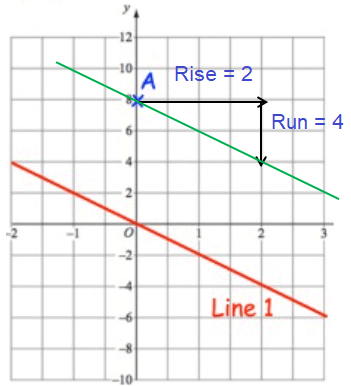
Equation of line passes through the point A will have the same slope 

y = -2x + 8

To check our equation, we select one of the point from the line that we have drawn. Say (2, 4)

Applying the point (2, 4) on the line :

4 = -2(2) + 8

4 = -4 + 8

4 = 4