FINDING DOMAIN AND RANGE OF A PIECEWISE FUNCTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Graph each of the following piecewise functions neatly and provide the requested information.
Problem 1 :
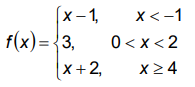
Solution :
|
First piece : y = x - 1 Since it is linear function, it should create a straight line. (-5, -6) (-4, -5) (-3, -4) and (-2, -3) |
|
Second piece :
y = 3
Since it is linear function, it should create a horizontal line.
|
Third piece : y = x + 2 Since it is linear function, it should create a straight line. (4, 6) (5, 7) (6, 8) and (7, 9) |
|
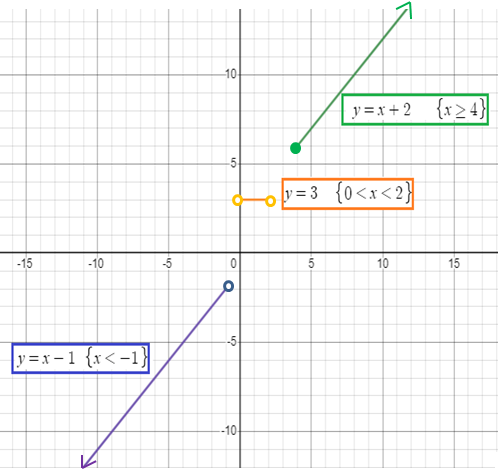
Domain = (-∞, -1), (0, 2) U [4, ∞)
Range = (-∞,∞)
Problem 2 :
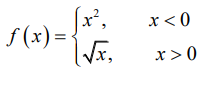
First piece :
y = x2
Since it is quadratic function, it must be a parabola, opens up.
|
x -2 -1 0 1 2 |
y 4 1 0 1 4 |
Second piece :
y = √x
It is a square root function, it is not defined for the negative values.
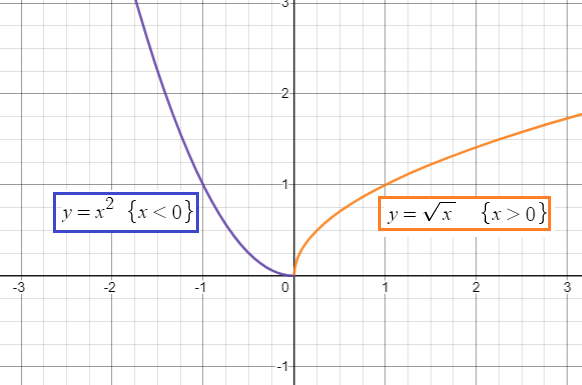
Domain = (-∞, ∞)
Range = (0,∞)
Problem 3 :
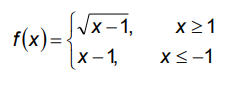
First piece :
y = √(x - 1)
It is a square root function, it is not defined for the negative values.
|
x 1 2 3 4 |
y 0 1 2 3 |
Points are (1, 0) (2, 1) (3, 2) and (4, 3).
|
Second piece : y = x - 1 It is a linear function (-4, -5) (-3, -4) (-2, -3) (-1, -2) |
|
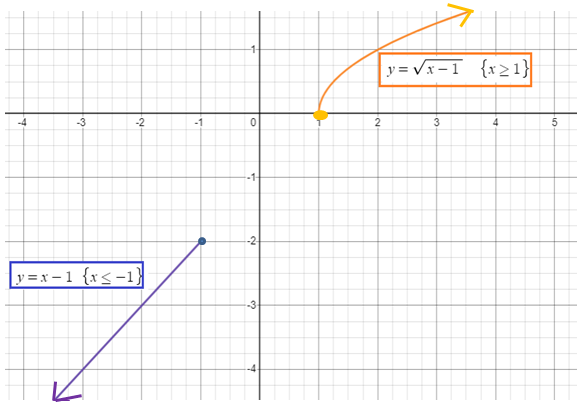
Domain = (-∞, -1] U [1,∞)
Range = (-∞, ∞)
Problem 4 :
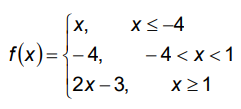
|
First piece : y = x Condition is x ≤ -4 It is a linear function. It will have the shape of straight line. (-6, -6) (-5, -5) (-4, -4) |
| ||
|
Second piece : y = -4 Condition is -4 < x < 1 It is a linear function, it is a horizontal line. | |||
|
Third piece : y = 2x - 3 Condition is x ≥ 1 (1, -1) (2, 1) (3, 3) |
|
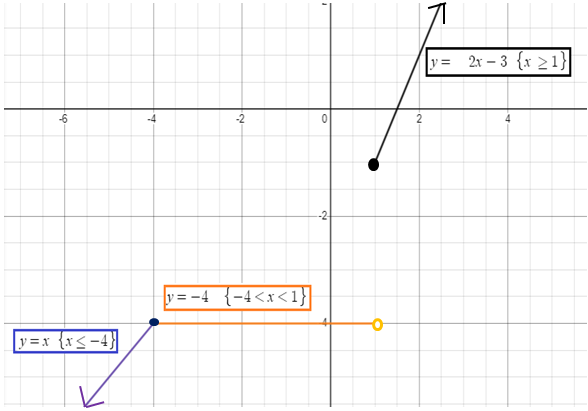
Domain = (-∞, ∞)
Range = (-∞, -4) U (-1,∞)
Problem 5 :
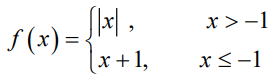
Solution :
First piece :
y = |x|
Since it is absolute value function, it will be in the shape of V.
vertex will be at (0, 0) and opens up.
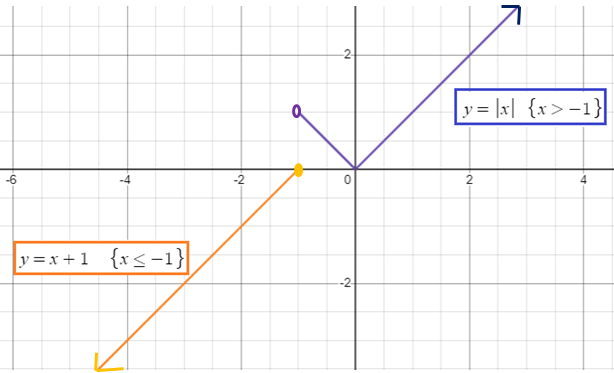
Domain = (-∞, ∞)
Range = (-∞,∞)
Find the domain and range of the piecewise function given below.
Problem 6 :
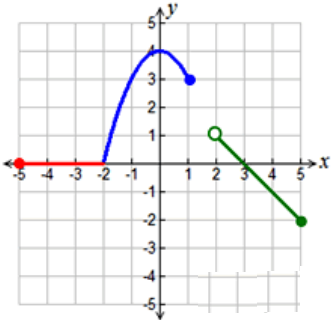
Solution :
Domain = [-5, 5]
Range = [-2, 4]
Problem 7 :
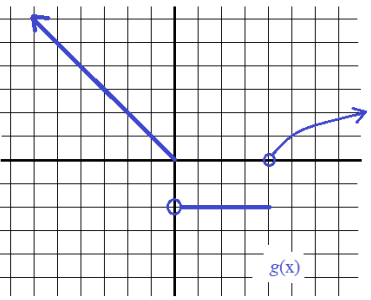
Solution :
Domain = (-∞, ∞)
Range = [-2, ∞)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling