FINDING DOMAIN AND RANGE OF A LOGARITHMIC FUNCTION

Finding domain :

Domain is set of all possible defined values of x. To find domain of logarithmic function, we can use the procedure given below.

Step 1 :

Take the argument and create the condition,

(ax + b) > 0

Step 2 :

Get the possible values of x from the above condition.

For example,

f(x) = log4 x x > 0
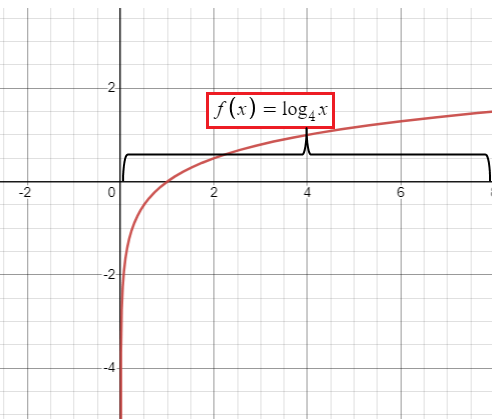f(x) = log4(x-2) x - 2 > 0 x > 2

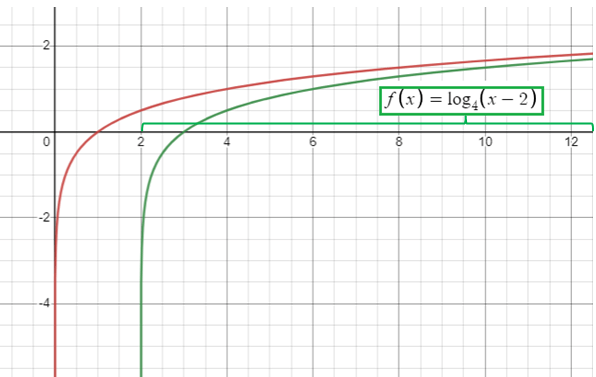Range :

Set of possible values of y is range. Always all real values.

Identify the domain and range of each. 

Problem 1 :

y = log₆ (x − 1) − 5

Solution :

Finding domain :

x − 1 > 0

x > 1

Domain is (1, ∞).

Finding range :

y = log₆ (x − 1) − 5

We have to the graph of parent function 5 units down. All real values is the range.

Problem 2 :

y = log₅ (x − 1) + 3

Solution :

Finding domain :

x − 1 > 0

x > 1

Domain is (1, ∞).

Finding range :

y = log₅ (x − 1) + 3

We have to the graph of parent function 3 units up. All real values is the range.

Problem 3 :

y = log₆ (x − 3) - 5

Solution :

Finding domain :

x − 3 > 0

x > 3

Domain is (3, ∞).

Finding range :

y = log₆ (x − 3) - 5

We have to the graph of parent function 5 units down. All real values is the range.

Problem 4 :

y = log₂ (x − 1) + 3

Solution :

Finding domain :

x − 1 > 0

x > 1

Domain is (1, ∞).

Finding range :

y = log₂ (x − 1) + 3

We have to the graph of parent function 3 units up. All real values is the range.

Problem 5 :

y = log₄ (x + 1) - 4

Solution :

Finding domain :

x + 1 > 0

x > -1

Domain is (-1, ∞).

Finding range :

y = log₄ (x + 1) - 4

We have to the graph of parent function 4 units down. All real values is the range.

Problem 6 :

y = log₄ (3x + 11) - 5

Solution :

Finding domain :

3x + 11 > 0

x > -11/3

Domain is (-11/3, ∞).

Finding range :

y = log₄ (3x + 11) - 5

We have to the graph of parent function 5 units down. All real values is the range.

Problem 7 :

y = log₅ (2x + 2) + 5

Solution :

Finding domain :

2x + 2 > 0

x > -2/2

Domain is (-1, ∞).

Finding range :

y = log₅ (2x + 2) + 5

We have to the graph of parent function 5 units up. All real values is the range.