FINDING DOMAIN AND RANGE FROM THE GRAPH OF AN EXPONENTIAL FUNCTION

Exponential function will be in any of the following forms.

y = b^x

(or)

y = ab^x

(or)

y = ab^x-h + k

Domain :

Domain of exponential function is all real values (-∞, ∞).

Range :

(k, ∞) or (-∞, k) can be any one of them, based on exponential growth or decay can be decided.

Exponential growth or decay :

If b > 0 for growth and 0 < b < 1 when it is decay

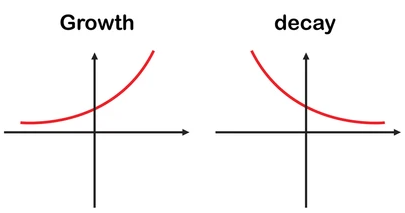
Horizontal asymptotes :

The exponential function which is in the form

y = ab^x-h + k

x = k is the horizontal asymptote.

Identify the domain and range for each graphed exponential function.

Problem 1 :

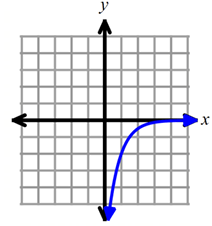
Solution :

Domain is all real numbers (-∞, ∞).

By finding horizontal asymptote, it is simple to fix the range. When we observe the graph, the horizontal asymptote is y = 0.

So, the range is (-∞, 0).

Problem 2 :

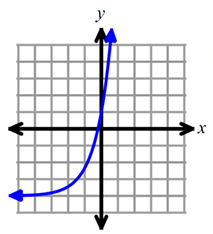
Solution :

Domain is all real numbers (-∞, ∞).

By finding horizontal asymptote, it is simple to fix the range. When we observe the graph, the horizontal asymptote is y = -4.

So, the range is (-4, ∞).

Problem 3 :

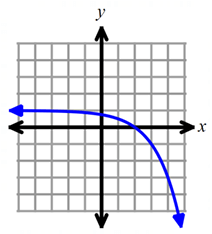
Solution :

Domain is all real numbers (-∞, ∞).

When we observe the graph, the horizontal asymptote is y = 1.

So, the range is (-∞, 1).

Problem 4 :

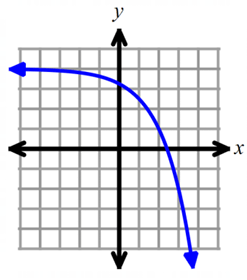
Solution :

Domain is all real numbers (-∞, ∞).

When we observe the graph, the horizontal asymptote is y = 4.

So, the range is (-∞, 4).

Problem 5 :

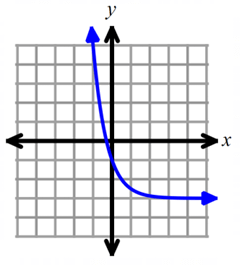
Solution :

Domain is all real numbers (-∞, ∞).

When we observe the graph, the horizontal asymptote is y = -3.

So, the range is (-3, ∞).

Graph the functions for the given table shown for each questions.

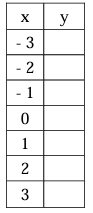
i) Is the function increasing or decreasing

ii)  Find the domain and range of the function.

Problem 6 :

f(x) = 4^x

Solution :

By applying the values of x one by one from the table.

When x = 3

f(x) = 4^x

f(3) = 4³

= 64

(-3, 1/64) (-2, 1/16) (-1, 1/4) (0, 1) (1, 4) (2, 16) and (3, 64)

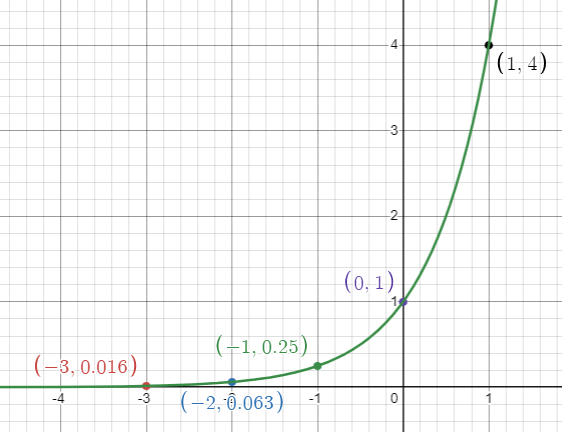
i) By observing the graph from left to right, it is going up. Then it is increasing function.

Horizontal asymptote is y = 0

ii) Domain is all real numbers (-∞, ∞).

Range is (0, ∞).

Problem 7 :

f(x) = 0.4^x

Solution :

By applying the values of x one by one from the table.

When x = 3

f(x) = 0.4^x

f(3) = (0.4)³

= 0.064

Plotting the points, (-3, 1/0.064) (-2, 1/0.16) (-1, 1/0.4) (0, 1) (1, 0.4) (2, 0.16) (3, 0.064).

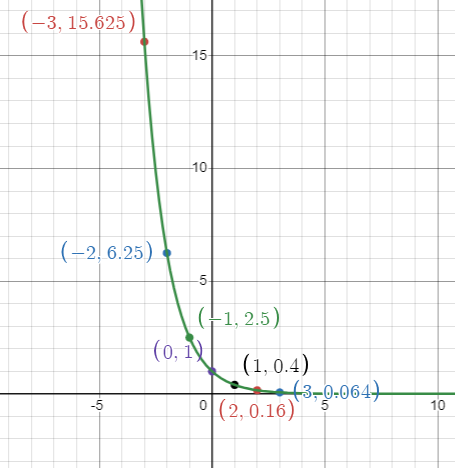
i) By observing the graph from left to right, it is falling down. Then it is decreasing function.

Horizontal asymptote is y = 0

ii) Domain is all real numbers (-∞, ∞).

Range is (0, ∞).