FINDING DOMAIN AND RANGE FROM ORDERED PAIRS

Problem 1 :

Identify the domain and range of the given relation.

Then represent the relation using a graph and a mapping diagram.

 (-2, 3), (1, 2), (3, -1), (-4, -3)

Solution :

(-2, 3), (1, 2), (3, -1), (-4, -3)

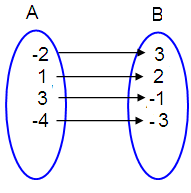
In the above arrow diagram, each element of A has image in B and also each element of A has only one image in A.

So, the given relation is a function.

Domain is the elements of A.

Domain = {-2, 1, 3, -4}

Range is the elements of B. 

Range = {3, 2, -1, -3}

Problem 2 :

(5, -2), (-3, -2), (3, 3), (-1, -1)

Solution :

(5, -2), (-3, -2), (3, 3), (-1, -1)

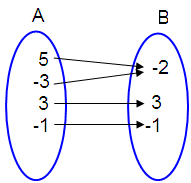
In the above arrow diagram, each element of A has image in B and also each element of A has only one image in A.

So, the given relation is a function.

Domain is the elements of A.

Domain = {5, -3, 3, -1}

Range is the elements of B.

Range = {-2, 3, -1}

Problem 3 :

(6, -1), (-2, -3), (1, 8), (-2, 5)

Solution :

(6, -1), (-2, -3), (1, 8), (-2, 5)

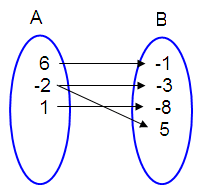
In the above arrow diagram, each element of A has image in B. But the element -2 in A has more than one image in B. (two images -3 and 5).

So, the given relation is a not function.

Problem 4 :

(-7, 4), (2, -5), (1, -2), (-3, 6)

Solution :

(-7, 4), (2, -5), (1, -2), (-3, 6)

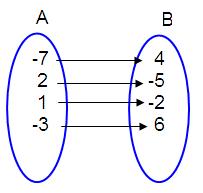
In the above arrow diagram, each element of A has image in B and also each element of A has only one image in A.

So, the given relation is a function.

Domain is the elements of A.

Domain = {-7, 2, 1, -3}

Range is the elements of B.

Range = {4, -5, -2, 6}

Problem 5 :

(5, 20), (10, 20), (15, 30), (20, 30)

Solution :

(5, 20), (10, 20), (15, 30), (20, 30)

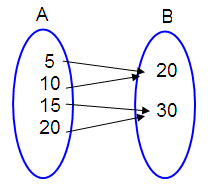
In the above arrow diagram, each element of A has image in B and also each element of A has only one image in A.

So, the given relation is a function.

Domain is the elements of A.

Domain = {5, 10, 15, 20}

Range is the elements of B.

Range = {20, 30}

Problem 6 :

(4, -2), (4, 2), (16, -4), (16, 4)

Solution :

(4, -2), (4, 2), (16, -4), (16, 4)

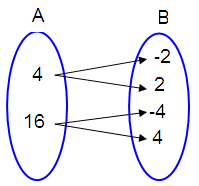
In the above arrow diagram, each element of A has image in B. But the element 4 and 16 in A has more than one image in B. (four images -2, 2 and -4, 4).

So, the given relation is a not function.

Problem 7 :

What is the domain of the relation given by the ordered pairs (-4, 2), (-1, -3), (1, 4), (1, -3), and (2, 1)?  

A)  -3, 1, 2 and 4        B)   -4, -1, 1, and 2

C) -4, -3, -1, and 2       D) -4, -3, -1, 1, and 2

Solution :

The domain of the relation is option B -4, -1, 1, and 2.