FINDING DIRECTION ANGLE OF A VECTOR

The direction angle θ of a vector v is the angle formed from the x-axis counterclockwise to the ray along which v lies.

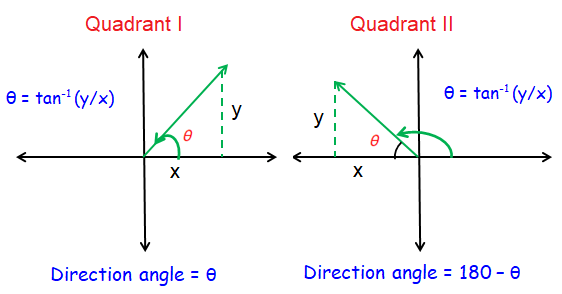
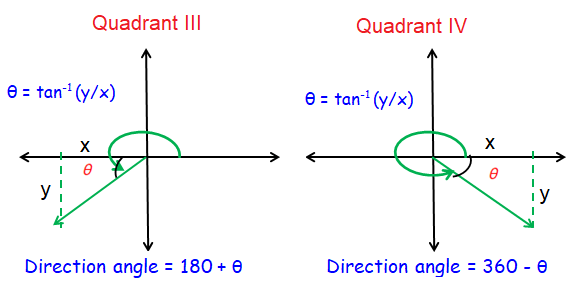
Given the initial and terminal points, find the following information for each vector: Component form, direction angle.

Problem 1 :

Solution:

Component form:

(C₁, C₂) = (1, -9) and (D₁, D₂) = (2, 1)

V = <D₁ - C₁, D₂ - C₂>

V = <(2 - 1), (1 + 9)>

V = < 1, 10 >

Direction angle:

We know that (1, 10) lies in quadrant I. Thus, the direction of the given vector is

θ = α 

θ = 84.29°

Problem 2 :

Solution:

Component form:

(C₁, C₂) = (9, -6) and (D₁, D₂) = (4, -7)

V = <D₁ - C₁, D₂ - C₂>

V = <(4 - 9), (-7 + 6)>

V = < -5, -1 >

Direction angle:

We know that (-5, -1) lies in quadrant III. Thus, the direction of the given vector is

θ = α + 180°

θ = 11.31° + 180°

θ = 191.31°

Problem 3 :

Solution:

Component form:

(P₁, P₂) = (-2, 1) and (Q₁, Q₂) = (-1, 3)

V = <Q₁ - P₁, Q₂ - P₂>

V = <(-1 + 2), (3 - 1)>

V = < 1, 2 >

Magnitude:

We know that (1, 2) lies in quadrant I. Thus, the direction of the given vector is

θ = α 

θ = 63.43°

Problem 4 :

Solution:

Component form:

(A₁, A₂) = (-6, -1) and (B₁, B₂) = (-5, 10)

V = <B₁ - A₁, B₂ - A₂>

V = <(-5 + 6), (10 + 1)>

V = < 1, 11 >

Magnitude:

We know that (1, 11) lies in quadrant I. Thus, the direction of the given vector is

θ = α 

θ = 84.81°

Problem 5 :

Solution:

Component form:

(R₁, R₂) = (-1, -7) and (S₁, S₂) = (7, -1)

V = <S₁ - R₁, S₂ - R₂>

V = <(7 + 1), (-1 + 7)>

V = < 8, 6 >

Magnitude:

We know that (8, 6) lies in quadrant I. Thus, the direction of the given vector is

θ = α 

θ = 36.87°