FINDING CRITICAL POINTS

To find critical numbers, we have to use steps given below.

Step 1 :

Find the first derivative.

Step 2 :

Equate the first derivative to 0.

Step 3 :

Solve for the variable. From this, we can understand that slope will be zero at these positions.

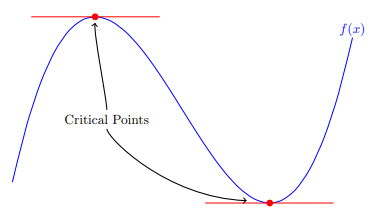
Use Calculus to find the CRITICAL POINTS of each of the following functions:

Problem 1 :

y = x² - 6x + 5

Solution :

Let f(x) = x² - 6x + 5

f'(x) = 2x - 6(1) + 0

f'(x) = 2x - 6

f'(x) = 0

2x - 6 = 0

2x = 6

x = 3

The curve will flatten at the x-coordinate 3. So, the critical number is x = 3.

Problem 2 :

y = x³/(x² - 1)

Solution :

Problem 3 :

f(x) = csc x ; [-π, π]

Solution :

f(x) = csc x

f'(x) = -csc x cot x

f'(x) = 0

-csc x cot x = 0

Problem 4 :

f(x) = e^x - x

Solution :

f(x) = e^x - x

f'(x) = e^x - 1

f'(x) = 0

e^x - 1 = 0

e^x = 1

x = ln (1)

x = 0

So, the critical number is x = 0.

Problem 5 :

f(x) = 6x⁵ + 33x⁴ - 30x³ + 100

Solution :

f(x) = 6x⁵ + 33x⁴ - 30x³ + 100

f'(x) = 30x⁴ + 132x³ - 90x² + 0

f'(x) = 30x⁴ + 132x³ - 90x²

f'(x) = 0

30x⁴ + 132x³ - 90x² = 0

3x²(10x² + 44x - 30) = 0

x = 0 and 10x² + 44x - 30 = 0

5x² + 22x - 15 = 0

5x² + 25x - 3x - 15 = 0

5x(x + 5) - 3(x + 5) = 0

(5x - 3) (x + 5) = 0

5x - 3 = 0, x + 5 = 0 

x = 3/5 and x = -5

So, the critical points are x = 0, -5 and 3/5.

Problem 6 :

f(x) = 4x³ - 9x² - 12x + 3

Solution :

f(x) = 4x³ - 9x² - 12x + 3

f'(x) = 4(3x²) - 9(2x) - 12(1) + 0

f'(x) = 12x² - 18x - 12

f'(x) = 0

12x² - 18x - 12 = 0

6(2x² - 3x - 2) = 0

2x² - 3x - 2 = 0

(x - 2)(2x+1) = 0

x = 2 and x = -1/2

So, the critical numbers are x = 2 and -1/2

Problem 7 :

f(x) = 2/(t² - 4)

Solution :

f(x) = 2/(t² - 4)

f(x) = 2(t² - 4)^-1

f'(x) = -2(t² - 4)^-2(2t - 0)

f'(x) = -4t (t² - 4)^-2

f'(x) = 0

-4t (t² - 4)^-2 = 0

t = 0

So, the critical number is x = 0.

Problem 8 :

f(x) = (ln x)²

Solution :

f(x) = (ln x)²

f'(x) = 2 ln x (1/x)

f'(x) = 2 (ln x/x)

f'(x) = 0

2 (ln x/x) = 0

ln x = 0

ln x = ln 1

x = 1

So, the critical number is x = 1

Problem 9 :

f(x) = 2 sin(x/2) where [-2π, 2π]

Solution :

f(x) = 2 sin(x/2)

f'(x) = 2 cos (x/2) (1/2)

f'(x) = cos (x/2)

f'(x) = 0

cos (x/2) = 0

x/2 = cos^-1(0)

x/2 = -π/2 and π/2

x = -π and π

So, the critical numbers are x = -π and π

Problem 10 :

f(x) = x² ln (x)

Solution :

f(x) = x² ln (x)

u = x²  and v = ln x

u' = 2x and v' = 1/x

d(uv) = uv' + vu'

= x² (1/x) + ln x(2x)

= x + 2x ln x

f'(x) = x(1 + 2 ln x)

f'(x) = 0

x(1 + 2 ln x) = 0

x = 0

1 + 2 ln x = 0

2 ln x = -1

ln x = -1/2

x = e^-1/2

x = 1/√e

So, the critical number is x = 1/√e.

Problem 11 :

The first derivative of the function 𝑓 is given by

f'(x) = sin²x/9 - (2/9)

How many critical values does f on the open interval (0, 10) ?

Solution :

f'(x) = sin²x/9 - (2/9)

f'(x) = 0

sin²x/9 - (2/9) = 0

sin²x/9 = 2/9

sin (x/9) = √(2/9)

sin x/9 = √2/3

(x/9) = sin^-1(√2/3)

We cannot solve ths.

Alternative way :

Using graphing calculator :

At critical points on the curve, we can draw horizontal tangent lines. Then, slope of horizontal line will be 0. 

Critical points of the original function f(x), will be the x-intercepts of derivative function f'(x).

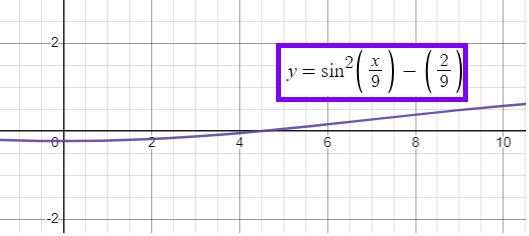
Number of x-intercepts is 1. So, number of critical numbers is 1.

Problem 12 :

If 𝑓 is a continuous, decreasing function on [0,10] with a critical point at (4, 2), which of the following statements must be false?

(A) 𝑓(10) is an absolute minimum of f on [0,10].

(B) 𝑓(4) is neither a relative maximum nor a relative minimum.

(C) 𝑓′(4) does not exist

(D) 𝑓′(4) = 0            (E) 𝑓'(4) < 0

Solution :

The critical number of the original function will be x-intercept of derivative function. So, f'(4) = 0 is correct.

Since it is decreasing function on [0, 10], it may have absolute minimum at f(10).

At f(4), the curve will flatten. so, it may have relative maximum or minimum.

f'(4) will be equal to 0, it is given less than 0. So, option E is false.