FINDING COTERMINAL ANGLES BETWEEN 0 AND 360

Coterminal angles are angles that have the same initial side and the same terminal sides. We determine coterminal angle of a given angle by adding or subtracting 360° or  2π.

Find a positive and a negative coterminal angle for each given angle.

Example :

326°

Solution :

Drawing 326° in the xy-plane, we get

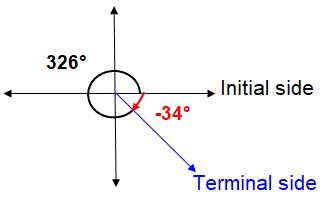
Keeping the initial side and terminal side as it is, we have to cover 34° in the negative direction (clockwise direction).

Let θ' be the coterminal angle.

θ' = 326 - 360 ==> -34°

θ' = 360 + 326 ==> 686°

So, coterminal angles of 326° are  -34° and 686°.

Note : We can find many angles like this.

Find a coterminal angle between 0^º and 360^º.

Problem 1 :

-220^º

Solution :

-220^º

Write -220^º in terms of 360^º.

-220^º = -360^º + 140^º

So, the coterminal angle of -220^º is 140^º.

Problem 2 :

-335^º

Solution :

-335^º

Write -335^º in terms of 360^º.

-335^º = -360^º + 25^º

So, the coterminal angle of -335^º is 25^º.

Problem 3 :

-160^º

Solution :

-160^º

Write -160^º in terms of 360^º.

-160^º = -360^º + 200^º

So, the coterminal angle of -160^º is 200^º.

Problem 4 :

-295^º

Solution :

-295^º

Write -295^º in terms of 360^º.

-295^º = -360^º + 65^º

So, the coterminal angle of -295^º is 65^º.

Problem 5 :

615^º

Solution :

615^º

Write 615^º in terms of 360^º.

615^º = 360^º + 255^º

So, the coterminal angle of 615^º is 255^º.

Problem 6 :

660^º

Solution :

660^º

Write 660º in terms of 360^º.

660^º = 360^º + 300^º

So, the coterminal angle of  660^º is 300^º.

Problem 7 :

-555^º

Solution :

-555^º

Write -555^º in terms of 360^º.

-555^º = -360^º - 195^º

-195^º is a negative coterminal angle . To find positive coterminal angle

360^º - 195^º = 165^º 

So, the coterminal angle of -555^º is 165^º.

Problem 8 :

-320^º

Solution :

-320^º

Write -320^º in terms of 360^º.

-320^º = -360^º + 40^º

So, the coterminal angle of -320^º is 40^º.

Problem 9 :

735^º

Solution :

735^º

Write 735^º in terms of 360^º.

735^º = 2(360^º) + 15^º

735^º = 720^º + 15^º

So, the coterminal angle of 735^º is 15^º.

Problem 10 :

420^º

Solution :

420^º

Write 420^º in terms of 360^º.

420^º = 360^º + 60^º

So, the coterminal angle of 420^º is 60^º.

Problem 11 :

-660^º

Solution :

-660^º

Write -660^º in terms of 360^º.

-660^º = 2(-360^º) + 60^º

-660^º = -720^º + 60^º

So, the coterminal angle of -660^º is 60^º.

Problem 12 :

-180^º

Solution :

-180^º

Write -180^º in terms of 360^º.

-180^º = -360^º + 180^º

So, the coterminal angle of -180^º is 180^º.

Problem 13 :

560^º

Solution :

560^º

Write 560^º in terms of 360^º.

560^º = 360^º + 200^º

So, the coterminal angle of 560^º is 200^º.

Problem 14 :

-315^º

Solution :

-315^º

Write -315^º in terms of 360^º.

-315^º = -360^º + 45^º

So, the coterminal angle of -315^º is 45^º.

Problem 15 :

-345^º

Solution :

-345^º

Write -345^º in terms of 360^º.

-345^º = -360^º + 15^º

So, the coterminal angle of -345^º is 15^º.

Problem 16 :

568^º

Solution :

568^º

Write 568^º in terms of 360^º.

568^º = 360^º + 208^º

So, the coterminal angle of 568^º is 208^º.

Problem 17 :

-330º

Solution :

-330º

Write -330º in terms of 360º.

-330º = -360º + 30º

So, the coterminal angle of -330º is 30º.

Problem 18 :

-435^º

Solution :

-435^º

Write -435^º in terms of 360^º.

-435^º = 2(-360^º) + 285^º

-435^º = -720^º + 285^º 

So, the coterminal angle of -435^º is 285^º.

Problem 19 :

640^º

Solution :

640^º

Write 640^º in terms of 360^º.

640^º = 360^º + 280^º

So, the coterminal angle of 640^º is 280^º.

Problem 20 :

-442^º

Solution :

-442^º

Write -442^º in terms of 360^º.

-442^º = 2(-360^º) + 278^º

-442^º = -720^º + 278^º 

So, the coterminal angle of -442^º is 278^º.