FINDING CONCAVITY AND INFLECTION POINTS FOR A FUNCTION
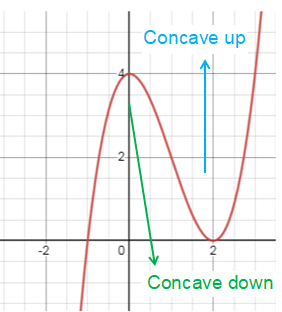
What is concave up and down ?
Concave upward :
If y = f(x) is a concave upward curve, then as x increases f'(x) either is of the same sign and increasing or changes sign from negative to positive.
In either case f'(x) is increasing and so f''(x) > 0 for a concave upward curve f''(x) > 0.
Concave downward :
An arc of a curve y = f(x) is called concave downward, then as x increases, f'(x) either is the same sign and decreasing or changes sign from positive to negative.
In either case f'(x) is decreasing and so f''(x) < 0, for a concave downward curve f''(x) < 0
Procedure to find Concavity and Points of Inflection
To find concavity of a function y = f(x), we will follow the procedure given below.
Step 1 :
Find the first derivative f '(x). By equating the first derivative to 0, we will receive critical numbers.
Step 2 :
Find the second derivative, that is f ''(x). Equate the second derivative f ''(x) = 0.
Apply the values that we are deriving from the second derivative in the number line and decompose into intervals.
Step 3 :
From each interval, by applying one of the values in the second derivative, if we receive the second derivative.
- f''(x) > 0, then the function f(x) is concave up in the interval.
- f''(x) < 0, then the function f(x) is concave down in the interval.
Point of inflection :
A point of inflection is a point at which a curve is changing
concave upward to concave downward
or
concave downward to concave upward
A curve y = f(x) has one of its points x = c as an inflection point, if
i) f''(c) = 0 or is not defined and
ii) f''(x) changes sign as x increases through x = c.
To find the point of inflection, we will follow the procedure given below.
Step 1 :
Equate the second derivative to 0, that is f ''(x) = 0
x = a, b
Step 2 :
(a, f(a)) and (b, f(b)) will be point of inflections.
For each problem, find the x - coordinates of all points of inflection, find all discontinuities, and find the open intervals where the function is concave up and concave down.
Problem 1 :
y = x3 - 3x2 + 4
Solution :
y = x3 - 3x2 + 4
Let y = f(x)
f(x) = x3 - 3x2 + 4
f'(x) = 3x2 - 6x
f''(x) = 6x - 6
f''(x) = 6(x - 1)
6(x - 1) = 0
x = 1
Decomposing into intervals
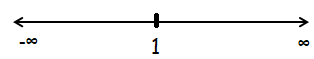
|
Intervals (-∞, 1) |
f''(x) = 6(x - 1) x = 0 ∈ (-∞, 1) |
Sign of f ''(x) f'' (0) = 6(0 - 1) f'' (0) > 0 Concave up |
|
(1, ∞) |
x = 2 ∈ (-∞, 1) |
f'' (2) = 6(2 - 1) f'' (0) < 0 Concave down |
Since the given is a polynomial function, it is continuous everywhere.
In f '' (x), changes its sign, there must be point of inflection.
When x = 1
f(1) = 13 - 3(1)2 + 4
= 1 - 3 + 4
= 2
So, the point of inflection is (1, 2).
Problem 2 :
y = x3 - 2x2 - 2
Solution :
y = x3 - 2x2 - 2
Let y = f(x)
f(x) = x3 - 2x2 - 2
f'(x) = 3x2 - 4x
f''(x) = 6x - 4
6x - 4 = 0
x = 2/3
|
Intervals (-∞, 2/3) |
f''(x) = 2(3x - 2) x = 0 ∈ (-∞, 2/3) |
Sign of f ''(x) f'' (0) = 2(-2) f'' (0) < 0 Concave down |
|
(2/3, ∞) |
x = 2 ∈ (-∞, 1) |
f'' (2) = 12 - 4 f'' (2) > 0 Concave up |
Since the given is a polynomial function, it is continuous everywhere.
In f '' (x), changes its sign, there must be point of inflection.
When x = 2/3
f(2/3) = (2/3)3 - 2(2/3)2 - 2
= 8/27 - 8/9 - 2
= (8 - 24 - 54)/27
= -70/27
So, the required point of inflection is (2/3, -70/27).
Problem 3 :
y = x4 + x3 - 3x2 + 1
Solution :
Let f(x) = x4 + x3 - 3x2 + 1
f '(x) = 4x3 + 3x2 - 6x + 0
f '' (x) = 12x2 + 6x - 6
f '' (x) = 0
6(2x2 + x - 1) = 0
6(2x - 1)(x + 2) = 0
x = 1/2 and x = -2
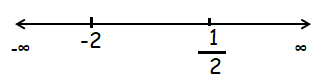
(-∞, -2), (-2, 1/2) and (1/2, ∞)
|
Intervals (-∞, -2) |
f''(x) = (2x-1)(x+2) x = -3 ∈ (-∞, -2) |
Sign of f ''(x) f'' (-3) = -7(-1) = 7 f'' (-3) > 0 Concave up |
|
(-2, 1/2) |
x = 0 ∈ (-2, 1/2) |
f'' (0) = -1(2) = -2 f'' (0) < 0 Concave down |
Since the given is a polynomial function, it is continuous everywhere.
In f '' (x), changes its sign, there must be point of inflection.
When x = -2
f(-2) = (-2)4 + (-2)3 - 3(-2)2 + 1
= 16 + 8 - 12 +1
= 25 - 12
= 13
When x = 1/2
f(1/2) = (1/2)4 + (1/2)3 - 3(1/2)2 + 1
= 1/16 + 1/8 - 3/4 + 1
= (1 + 2 - 12 + 16)/16
= 7/16
So, the point of inflection are (-2, 13) and (1/2, 7/16).
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling